BIOTENSEGRITY: A DIFFERENT WAY OF THINKING       Graham Scarr    request copy

In: Pilat, A., (ed.)., Fascia: scientific advances; Proceedings of the 28th Jornadas de Fisioterapia Conference, March 1-3, Madrid: Escuela Universitaria de Fisioterapia de la Once; 2018:167-180.

Introduction

Tensegrity as a structural design principle has been around since the middle of the twentieth century and is currently seeing a huge expansion in interest. From early forays into a new form of sculpture it is now incorporated into architecture and robots destined for the exploration of space, and attracting the attention of biologists and clinicians in their quest to better understand functional anatomy and movement – biotensegrity.

The biotensegrity concept is different to what has gone before because it is based on the fundamental rules of physics first and from which everything else is derived. It recognizes that complex living structures are the result of interactions between some basic self-organizing principles and that Natures ‘strategy for design’ is already built into the dynamic architecture of the system. A principle of structural organization that extends from the smallest of molecules to the complete organism and uses the simplest of models to better understand their complex dynamics1-5.

The problem with mechanics

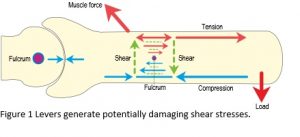At some point in our lives, we have all been taught that the body moves through a system of levers, but the problem with levers is that they generate bending moments, shear stresses and potentially damaging stress concentrations and it is most unlikely that developing tissues would be able to withstand the disastrous consequences of these (Figure 1).2 In addition, the nervous system is incapable of controlling the huge complexity of joint movements on its own and far too slow in responding to the rapidly changing conditions found in such activities as running and chewing food, which thus leaves a massive gap in our understanding of motion.3,4,6

The whole idea of levers as an explanation of joint mechanics has been around for more than three-hundred years, since the mathematician Giovanni Borelli compared the anatomy of human movement with man-made machines of the day. In 1680, he wrote a book describing his system of levers as an explanation for joint motion, and this has remained essentially unchanged to the present day. Biomechanics has thus tended to examine joints in isolation, where the anatomy is simplified down to some semi-arbitrary minimum and the data used is frequently the result of guess-work. It ignored the shear stresses, paid little attention to the connective tissues that link multiple joints together and overlooked the inadequacies of the nervous system.

Lever theory is based on the laws of Classical mechanics as formulated by Galilei, Newton and Hooke, amongst others, but these rules were discovered on inanimate objects and don’t easily apply to the non-linear dynamics of living tissues. So, what started off as a theory of human movement that has never been proved has become established as a principle of biomechanics simply because there has been nothing else to replace it – until now! There is nothing wrong with classical mechanics but its application to biology needs revision.

Biotensegrity

The biotensegrity model considers the relationship between every part of an organism and the mechanical system that integrates them into a complete functional unit. It is a simple re-evaluation of anatomy as a network of structures under tension and others that are compressed, parts that pull things together and others that keep them apart, basic physics (Figure 2).

Tensegrity structures are strong, light in weight, flexible and resilient. They can move with the minimum of effort and always return to the same position of equilibrium. Each part is integrated with all the others and has a mechanical influence on the whole system. When one part changes then everything around it also changes, which means that forces, power and information can be efficiently transmitted from one region to another.

At the simplest level, atoms interact with each other through the forces of attraction and repulsion, and they spontaneously organize themselves into the most stable and energy-efficient configurations to form rigid crystals and flexible molecules; and the same principles apply at every size scale. Tensegrity models are representations of those invisible forces, where ‘attraction and repulsion’ and ‘tension and compression’ are separated into the cables and struts, respectively, with the struts suspended or appearing to float within the tensioned network of cables.7 In the same way, we can consider the bones suspended within the tensioned network of muscles, fascia and other connective tissues because both the simple model and complex anatomy are formed through the same principles.

Basic principles

  1. The geodesic geometry, where these forces always act in straight lines but give rise to complex curvature at higher size-scales; and curvature is just another means of minimizing energy (Figure 2).
  2. The efficient close-packing of multiple parts into the smallest amount of space, where each part is structurally dependent on all those surrounding it.
  3. The principle of minimal-energy where everything happens in the simplest and most efficient way possible. Because these forces always act in straight lines, the material properties of these structures can then be efficiently optimized towards their function. The entire structure settles in a state of balanced equilibrium and minimal-energy, and although the dynamics of living systems are constantly changing and far from equilibrium, the same principles apply. There is more about non-equilibrium mechanics within a related article in this issue.8

Hierarchies and the global heterarchy

Structural hierarchies are an inherent capability of tensegrity configurations and ubiquitous in biology, where each part is made from smaller parts and which themselves are made from even smaller parts.9,10 They reduce weight, maintain strength, optimize the load-bearing ability, dissipate potentially damaging stresses and connect every level from the simplest molecule to the most complex organism with the entire system acting as a functional unit. As an example, the model in Figure 2a is constructed from six struts and twenty-four cables, where the end of each strut has four cables attached to it, which means that all the tensional stresses are concentrated on these single points. However, if we model each cable and strut as a chain of tensegrity structures, i.e. as a simple heterarchy (Figure 2b), and then consider the model in Figure 3 showing just the end of one of these struts with its four cables attached, we now see that these forces are now distributed over a much wider field and make the whole structure much stronger.

However, while anatomy is generally classified into a hierarchical system of top-down ‘large important structures followed by smaller and less significant ones’, such as an organ, tissue, cell, molecule sequence, it should be noted that all the sub-structures that form each one are equally important and part of a mutual relationship that is essential to the overall integrity. As each one influences the mechanical behaviour of all the others in the system, (top-down, bottom-up, in-out and in every direction) such organization warrants the term heterarchy as a more inclusive multi-directional descriptor, and this distinction is an important one in a biotensegrity context.11

Each part of the anatomy then becomes a modular unit nested within and dependent on all those surrounding it. Cells are nested within the extracellular matrix, muscle fibres are nested within the endomysial fascia surrounding them, and bones are nested within the tensioned network of muscles, fascia and other connective tissues, etc, etc.12

Underlying mechanics

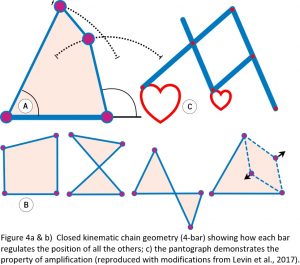Underlying all of this is the closed kinematic chain (CKC) organization, which constitutes the basic mechanics of tensegrity, where multiple anatomical ‘components’ or ‘bars’ are coupled into continuous mechanical loops with each one regulating the position and motion of all the others within the  heterarchy (Figure 4). Such a system is ubiquitous in biology and a simple and efficient mechanism that enables the controlled transfer and amplification (or reduction) of force, speed and kinetic energy throughout the body, and the pantograph drawing mechanism nicely illustrates this.13,14 Kinematics is about the geometry of motion, and the simplest shape that enables the structure itself to control this is the 4-bar mechanism where the length and position of each bar determines the position of all the others, and the angles between them define its mechanical properties.15

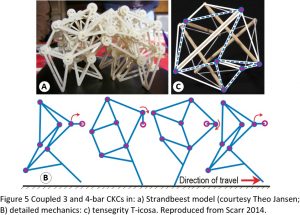Figure 5a,b shows a combination of 3 and 4-bar shapes in a model of the Strandbeest ‘creatures’ created by the artist Theo Jansen, and that walk along the beach in the Netherlands and are powered entirely by the wind. Each 3-bar mechanism forms a rigid triangle that allows the 4-bars to change shape and guide motion, and the same principle operates in the tensegrity model, where the 3-bar tension triangles provide the stability that allows the 4-bar modules to change shape and control movement (Figure 5c). Such closed-chain systems can actually have any number of bars oriented in any direction, and which increase the number of degrees of freedom and motion possibilities but are unstable on their own. The 4-bars, however, couple them into a functional unit that enables the structure itself to regulate motion.

At first sight, these closed-chain systems can look like complex levers, but this is not the case in a biotensegrity context where each bar can be either tensioned or compressed, and each pin-joint is made from smaller tensegrity modules coupled together within the overall organization (Figure 3). The changing position of each one can then influence the position of others some distance away and throughout the entire system, and enable each structure to remain completely stable throughout motion, i.e. it is dynamically stable.

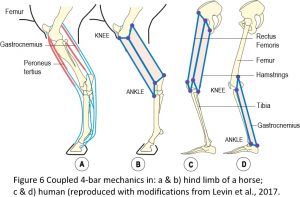Closed-chain kinematics explains how the jaws of fish can open, catch prey and close within a period of just twenty-five milliseconds, and how the Mantis shrimp can strike its prey with a force of fifteen-hundred Newtons.13 It is also illustrated in the cruciate ligaments within the knee and multi-articular muscles in the limbs of horses and humans (Figure 6).16,17 Here, the 4-bar geometry is clear to see in the flexor and extensor muscles that couple two or more joints and act together to guide, stabilize and regulate joint motion. A similar situation is found in humans where the rectus femoris forms a 4-bar with the pelvis, femur and tibia, and the hamstring muscles form a similar mechanism posteriorly, with both systems acting together to coordinate motion of the hip and knee joints. The gastrocnemius also forms another 4-bar system that links with the rectus and hamstring 4-bars through the femur and tibia.14

These bi-articular muscles are particularly interesting because they can act over the full range of both joints at the same time, or restrict the motion of one whilst enhancing that of the other, with isometric contractions enabling them to transfer forces and power from one part of the system to another and in ways that would otherwise be impossible. They also further challenge the usual distinction between agonist and antagonist muscles.

For example, jumping from a standing position using just the muscles that cross the ankles means that only a small amount of force can be used to plantar flex the foot. However, jumping from a semi-crouched position where the contraction of the gluteus and hamstrings in extending the hip is directly coupled with the activation of rectus femoris to extend the knee, and gastrocnemius to plantar flex the ankle, means that the force of all these muscles is effectively transferred to the ankle and foot through this closed-chain system and causes a much greater amount of motion. The same principle is also likely to apply to rock climbers who support and move their entire body weight from just the tips of their fingers, and throughout the body.14

CKC organization is a ubiquitous, mechanically-efficient and evolutionary-conserved arrangement in biology that is also influencing the way we think about embryological development and evolution,18 and as the underlying mechanics of tensegrity, changing our views on biomechanics in general.1-3

Non-linearity

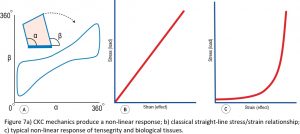One of the characteristics that emerges out of CKC geometry is the property of non-linearity (Figure 7a), and which is easy to see when plotting the relationship between the angles alpha and beta as the structure changes shape and forms this continuous non-linear curve, but this characteristic is frequently disregarded in biomechanical analyses. Standard biomechanical theory generally considers the relationship between stress and strain to be a linear one (Figure 7b), while the mechanics of tensegrity and biological systems conform more to the non-linear curve of Figure 7c and are likely to operate more within the initial ‘horizontal’ region, where they would be consuming much less energy and operating more efficiently than within the more vertical part. All of which suggests that the relevance of Young’s Modulus (stress/strain) in a biological context is somewhat questionable because it will be constantly changing as the system responds to variations in load. Living tissues conform more to the newly emerging physics of soft-matter than classical theory.19

Auxetics

In addition, the emergent property of auxetics demonstrates a different stress/strain relationship to most man-made materials, where a structure that is lengthened becomes thinner in the middle and fatter when it is shortened (positive Poisson ratio). Auxetic structures do the opposite and become fatter when they are lengthened and thinner when shortened, and this is evident in the tensegrity model, where the entire structure expands and contracts in every direction.1,2,20 This auxetic response has also been described in the behaviour of foams, bones, tendons and skin, and together with the examples described above, suggests that many of our ideas about biomechanics need revising.21

Transfer of information

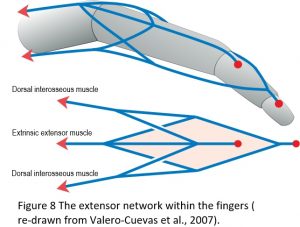One of the most important features of tensegrity in biological movement is the way in which the CKC organization couples the entire structural system into a complete mechanical unit, and as a consequence, enables forces, power and information to be transferred from one part of the body to another. The extensor tendon network within the fingers nicely illustrates this principle with the 4-bar mechanism known as Winslow’s rhombus (Figure 8), and where there are no muscles contained within the fingers themselves. Movement is thus dependent entirely on the action of muscles located at some distance in the forearm and hand and which transmit their tensional force through long tendons, yet there are simply not enough muscles to control all the different joint positions on their own. Their motion only becomes possible because of the particular way in which the soft-tissue network is organized.22

When these muscles contract, they alter the distribution of forces within the extensor tendon network and change the CKC (tensegrity) geometry, which then causes the phalanges to move in relation to each other. So, while it is muscle activity that changes the balance of tension within the soft-tissue network, so it is the structure itself that is processing the information (force and direction) and switching the position of the bones in relation to each other. The soft-tissue network is thus performing its own logic computations and enabling movements that were once attributed solely to the nervous system; and this transference of energy, forces and information is also intrinsic to tensegrity.23

While we have looked at some characteristics of the biotensegrity concept and shown how this is relevant to human dynamics, we can now examine one more example of this relationship and show how it relates to treatment.

The temporo-mandibular joint

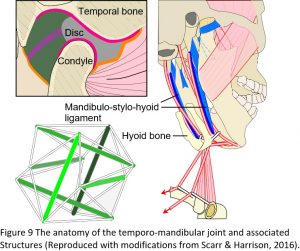The temporo-mandibular or jaw joint (TMJ) is commonly described as a hinge joint and third-class lever, where the mandibular condyles compress the discs against the glenoid fossa of the temporal bones and the nervous system controls movement; but the problem with this model is that a heavily compressed disc leads to degeneration and pathology of the joint (Figure 9). However, almost every book and article written on the TMJ starts with something like: ‘the jaw causes more problems than any other joint in the body and is the least understood’, and then goes on to describe it as a lever system, knowing full well that a heavily compressed disc (the inevitable result of a lever mechanism) leads to problems, but until recently, there has been no real alternative.24,25

Suspended bones

It is well recognized that the hyoid bone is suspended within the muscles, ligaments and fascia that surround it and acts as a stabilizer that allows the front of the mandible to be pulled downwards during mouth opening. Conversely, the mandible is also a stabilizer that allows the hyoid to be pulled up and forwards, through the same muscles, and influence the pharyngeal tissues during swallowing. Over the last few years, it has been recognized that there is a particular thickening of the fascia between the hyoid bone and angle of the mandible, called the mandibulo-stylo-hyoid ligament, and this is now considered to be highly significant from a biotensegrity perspective.  As the hyoid bone is pulled downwards by the sternohyoid and omohyoid muscles, it is likely to tension the mandibulo-stylo-hyoid ligaments, which then pull the angle of the mandible downwards, lower the condyles (because both are in line with the tension force) and takes the pressure off the discs during both mouth opening and closing.

The biotensegrity model then shows how the mandible can be suspended within the tensioned network of muscles, ligaments and fascia, where these forces are acting in every direction of space (CKCs) and contributing to placing the bone in any position during movement, as well as taking the pressure off the discs and stabilizing the joint. It also shows how the nervous/muscular systems can contribute to regulating the amount of pressure exerted across the articular surfaces, and how the structure itself can respond instantly to unexpected perturbations during eating and chewing, i.e. they are all working in synergy with each other.25

Therapeutic touch

Of course, all the above descriptions are huge simplifications of very complex structures but the same basic principles are operating in every case. Many dentists now recognize the importance of the biotensegrity model and have been using it to develop new methods and techniques for treating both the dentition and TMJ. There is also much that can be done by the manual therapist who works directly on the soft tissues but inevitably has an influence on the ‘islands of compression’ (bones) suspended within them, and vice versa, and which in the case of the TMJ include far more than just the ‘jaw’. The scalp, facial, cervical, tongue and pharyngeal tissues are intimately related to it, as are the cranial bones, hyoid, sternum, clavicle, ribcage, spine and beyond…26,27

A therapeutic contact that alters the material properties of the tissues (CKC geometry) is also likely to change the pattern of sensory neural signals generated by the mechano-receptors within them, and which in turn would influence muscle activity through neural reflex loops. From a biotensegrity perspective that recognizes such integration, it is taken for granted that a change in one part must have a reciprocal influence on others some distance away, and that this exchange of information is operating simultaneously at every size scale: nano, micro, meso and macro.

Conclusion

The biotensegrity concept is different to what has gone before because it is based on the fundamental rules of physics first and from which everything else is derived, and thus represents a paradigm shift in the way that we think about the human body. It is part of the basic science that underpins clinical reasoning, where we no longer need to think of bones, muscles and fascia as isolated structural entities but as contributors to a body-wide kinematic system that couples every part into a unified whole.

Biotensegrity looks at morphological complexity through the geometry of its architecture and appreciates this as a simple and energy-efficient arrangement that has refined itself over millions of years. A constantly evolving system that enables each part to move with the minimum of effort and powers the dynamism that we recognize as life.

References

  1. Levin SM. The tensegrity truss as a model for spine mechanics: biotensegrity. Journal of Mechanics and Medicine in Biology. 2002;2:375-88.
  2. Levin SM. Tensegrity: the new biomechanics. In: Hutson M, Ellis R. (eds.) Textbook of musculoskeletal medicine. Oxford: Oxford University Press; 2006.
  3. Kiely J, Collins DJ. Uniqueness of human running coordination: the integration of modern and ancient evolutionary innovations. Frontiers in Psychology. 2016;7, 262; doi: 10.3389/fpsyg.2016.00262.
  4. Wilson J, Kiely J.. The multi-functional foot in athletic movement: extraordinary feats by our extraordinary feet. Human Movement. 2016;17:15-20.
  5. Scarr G. Biotensegrity: the structural basis of life. Edinburgh: Handspring; 2014.
  6. Brown IE, Loeb GE. A reductionist approach to creating and using neuromuscular models. In: Winsters J, and Crago P. (eds.) Biomechanics and Neural Control of Posture and Movement. New York: Springer-Verlag; 2006;148-163.
  7. Heartney E. Kenneth Snelson: forces made visible. Massachusetts: Hard Press Editions; 2009..
  8. Scarr G. Health and Disease: what is the difference? In: Pilat, A., (ed.)., Fascia: scientific advances, Proceedings of the 28th Jornadas de Fisioterapia Conference, March 1-3, Madrid: Escuela Universitaria de Fisioterapia de la Once; 2018:219-225.
  9. Simon HA. The architecture of complexity. Proceedings of the American Philosophical Society. 1962;106:467-482.
  10. Zhang Z, Zhang YW, Gao H. On optimal hierarchy of load-bearing biological materials. Proceedings of the Royal Society B. 2011;278:519-525.
  11. Turvey MT, Fonseca ST. The medium of haptic perception: a tensegrity hypothesis. Journal of Motor Behavior. 2014;46(3):143-187.
  12. Clune J, Mouret JB, Lipson H. The evolutionary origins of modularity. Proceedings of the Royal Society B. 2013;280, 20122863; doi.org/10.1098/rspb.2012.2863.
  13. Claverie T, Chan E, Patek SN. Modularity and scaling in fast movements: power amplification in mantis shrimp. Evolution. 2011;65(2):443-61.
  14. Levin SM, Lowell de Solórzano S, Scarr G. The significance of closed kinematic chains to biological movement and dynamic stability. Journal of Bodywork and Movement Therapies, 2017;21:664-672.
  15. Muller M. A novel classification of planar four-bar linkages and its application to the mechanical analysis of animal systems. Philosophical Transactions of the Royal Society of London B. 1996;351(1340):689-720.
  16. Bradley J, FitzPatrick D, Daniel D, Shercliff T, O’Connor J. Orientation of the cruciate ligament in the sagittal plane. Journal of Bone and Joint Surgery. 1988;70-B:94-99.
  17. Van Ingen Schenau GJ. Proposed actions of bi-articular muscles and the design of hindlimbs of bi-and quadrupeds. Human Movement Science. 1994;13:665-681.
  18. Wainwright PC, Alfaro ME, Bolnick DI, Hulsey CD. Many-to-one mapping of form to function: a general principle in organismal design? Integrative and Comparative Biology. 2005;45:256-262.
  19. Hirst LS. Fundamentals of soft matter science. Boca Raton, Florida: CRC Press, Taylor & Francis Group; 2013.
  20. Castro-Arenas C, Ghersi I, Borsoi PD, Miralles M. Platonic tensegrities: dynamic aspects and characterization. In: Torres I, Bustamante J, Sierra D. (eds.), VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Santander, Colombia, October 26th -28th, 2016. IFMBE Proceedings, 2017;60. Singapore, Springer.
  21. Alderson A, Alderson KL. Auxetic materials. Journal of Aerospace Engineering. 2007;221:565-575.
  22. Valero-Cuevas FJ, Yi JW, Brown D, McNamara III RV, Paul C, Lipson H. The tendon network of the fingers performs anatomical computation at a macroscopic scale. Transactions on Biomedical Engineering. 2007;54(6 pt. 2):1161-1166.
  23. Ingber DE, Wang N, Stamenović D. Tensegrity, cellular biophysics and the mechanics of living systems. Reports on Progress in Physics. 2014;77(4), 046603; doi: 10.1088/0034-4885/77/4/046603.
  24. Scarr G, Harrison H. Resolving the problems and controversies surrounding temporo-mandibular mechanics. Journal of Applied Biomedicine. 2016;14:177-185.
  25. Scarr G, Harrison H. Examining the temporo-mandibular joint from a biotensegrity perspective: a change in thinking. Journal of Applied Biomedicine. 2017;15:55-62.
  26. Saccucci M, Tettamanti L, Mummolo S, Polimeni A, Festa F, Salini V, Tecco S. Scoliosis and dental occlusion: a review of the literature. Scoliosis. 2011;6, 15; doi: 10.1186/1748-7161-6-15.
  27. Sonnesen L. Associations between the cervical vertebral column and craniofacial morphology. International Journal of Dentistry. 2010; 29572:1-6; doi: 10.1155/2010/295728.