Defining Biotensegrity
The concept of tensegrity as a new structural principle really started in the 1940’s with Kenneth Snelson,Snelson who explored and developed it through sculpture, and Buckminster Fuller who considered it as part of a wider system of geometry. The application to living organisms began in the 1970’s with Stephen Levin, an orthopaedic surgeon who considered it from a structural, energetic and evolutionary perspective, and Donald Ingber who was then investigating the role of the cellular cytoskeleton in angiogenesis.
Many definitions have been proposed for tensegrity but they all vary according to the sculptural, engineering or biological interests of their authors. Engineers have introduced new terminology and mathematics suited to their purpose of making robotics and deployable structures in space, while biologists have approached the subject from first principles, experiment and energetic considerations. Definitions provide a foundation for further inquiry and both Snelson and Fuller developed their own essentially similar versions.
SNELSON: “Tensegrity describes a closed structural system composed of a set of three or more elongate compression struts within a network of tension tendons, the combined parts mutually supportive in such a way that the struts do not touch one another, but press outwardly against nodal points in the tension network to form a firm, triangulated, pre-stressed, tension and compression unit.”
FULLER: “Tensegrity describes a structural-relationship principle in which structural shape is guaranteed by the finitely closed, comprehensively continuous, tensional behaviours of the system and not by the discontinuous and exclusively local compressional member behaviours.”
 There is no standard method of naming tensegrity structures at the present time because artists, mathematicians, engineers and biologists take different approaches and use a variety of terminologies; and while it is assumed that developments in one field are directly transferable to another, examples in the literature show that this is not always the case. For example, engineers use a classification that is not directly applicable to living tissues, which prompted Levin to introduce the term ‘biotensegrity’ as a means of distinguishing biological tensegrity from its man-made engineering applications.
There is no standard method of naming tensegrity structures at the present time because artists, mathematicians, engineers and biologists take different approaches and use a variety of terminologies; and while it is assumed that developments in one field are directly transferable to another, examples in the literature show that this is not always the case. For example, engineers use a classification that is not directly applicable to living tissues, which prompted Levin to introduce the term ‘biotensegrity’ as a means of distinguishing biological tensegrity from its man-made engineering applications.
THE BIOTENSEGRITY MODEL
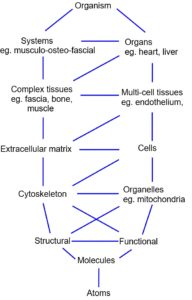
Most experimental work on biotensegrity has been carried out on cells, which are essentially complete organisms that can be examined individually, collectively, or in parts. Single cells are easily manipulated, abundant in variation and supply and there are few issues that might restrict their use; but multi-celled organisms such as humans are quite different. They consist of multiple heterarchical levels, with all the increases in complexity that might be expected, and examination of any part in isolation can be misleading. The use of dead tissues in biomechanical experiments thus has its limitations because they don’t behave exactly like living structures, and in-vivo experimentation is restricted due to practical and ethical issues. Generalizations from a ‘whole-body’ perspective have thus been reasoned from first principles (maths, geometry, mechanics and energetics) or inferred from models and observation.
Although the principles of tensegrity are easily demonstrated in simple models, they are built with components on the same size scale, and the essence of biotensegrity is structural and functional inter-dependency between components at multiple size scales; and the following should be considered from this perspective.
 The ‘simplest’ tensegrity model has 3-struts and is commonly referred to as the T3-prism (simplex or tripod); and is the first of an infinite series that continues with the T4-prism (quadruplex), T5-prism (pentaplex) and T6-prism (hexaplex) etc. Although they are called ‘prisms’ they all have a left or right-handed twist between their polygonal ends that corresponds with a class of structures called ‘antiprisms’ and conform to the formula:
The ‘simplest’ tensegrity model has 3-struts and is commonly referred to as the T3-prism (simplex or tripod); and is the first of an infinite series that continues with the T4-prism (quadruplex), T5-prism (pentaplex) and T6-prism (hexaplex) etc. Although they are called ‘prisms’ they all have a left or right-handed twist between their polygonal ends that corresponds with a class of structures called ‘antiprisms’ and conform to the formula:
angle of twist = 90o – 180o/n where n = number of struts.
Thus a T3-prism has a 30o twist between the ends, a T4-prism has a 45o twist and a T5-prism has a 54o twist etc.
 Pugh classified them as ‘cylindrical’ tensegrities and when joined end to end they form what can be called T-helixes. Tensegrity helixes are not continuous like springs, but form tubes with struts that are distinct, just like the components in biology (see Biology and Geodesics pages).
Pugh classified them as ‘cylindrical’ tensegrities and when joined end to end they form what can be called T-helixes. Tensegrity helixes are not continuous like springs, but form tubes with struts that are distinct, just like the components in biology (see Biology and Geodesics pages).
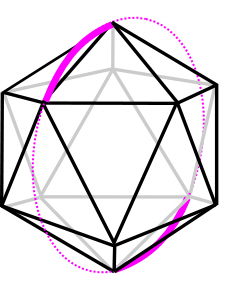
T3-prisms of opposite chirality can be reconfigured to form a 6-strut tensegrity with nodes (strut-ends) that almost, but not quite, correspond with the vertices of an icosahedron; Kenner classified this as a spherical tensegrity and it is commonly referred to as the Tensegrity-icosahedron, T6-sphere, T6-icosahedron and T-icosa.
The T-icosahedron is also sometimes described as the ‘expanded octahedron’ and ‘reducing cuboctahedron’, which relates to its place in the jitterbug – a model that demonstrates the changes in energy state from one position to another.
 Some people dispute naming this model as a tensegrity-icosahedron because its vertices do not match those of the platonic icosahedron, preferring instead to use the term ‘expanded-octahedron’ because of its symmetries (see Tom Flemons archive). Both models can contract towards the octahedron phase of the jitterbug (but only partially), and automatically expand back to the icosahedral phase. Leftheri Pavlides has produced an ‘elastegrity’ model that behaves similarly, and Borge Jessen described the ‘orthogonal icosahedron’ that closely matches the tensegrity model.
Some people dispute naming this model as a tensegrity-icosahedron because its vertices do not match those of the platonic icosahedron, preferring instead to use the term ‘expanded-octahedron’ because of its symmetries (see Tom Flemons archive). Both models can contract towards the octahedron phase of the jitterbug (but only partially), and automatically expand back to the icosahedral phase. Leftheri Pavlides has produced an ‘elastegrity’ model that behaves similarly, and Borge Jessen described the ‘orthogonal icosahedron’ that closely matches the tensegrity model.
 Jessen’s icosahedron is illustrated on YouTube and described in Wikipedia and Wolfram MathWorld. A correction is reported here, with detailed discussion here.
Jessen’s icosahedron is illustrated on YouTube and described in Wikipedia and Wolfram MathWorld. A correction is reported here, with detailed discussion here.
The T-icosa is the most important model from a biotensegrity perspective because of its multiple properties that relate to the minimal-energy efficiencies of the sphere and icosahedron, i.e. Biotensegrity looks at it from a much broader perspective.
A ‘higher-frequency’ tensegrity-icosahedron can also be made with 30 struts – T30-icosahedron or T30-sphere.
 This model sequence shows how the T-icosahedron as an ‘expanded octahedron’ can be developed from the octahedron, with the central struts passing through the middle of each other, followed by the struts and cables dividing, and the separated struts expanding into the 6-strut model. The term ‘expanded octahedron’ also relates to the octahedral phase of the jitterbug – a dynamic energy system that shows how these ‘energy shapes’ can transform from one to another.
This model sequence shows how the T-icosahedron as an ‘expanded octahedron’ can be developed from the octahedron, with the central struts passing through the middle of each other, followed by the struts and cables dividing, and the separated struts expanding into the 6-strut model. The term ‘expanded octahedron’ also relates to the octahedral phase of the jitterbug – a dynamic energy system that shows how these ‘energy shapes’ can transform from one to another.
Similarly, the term ‘reducing cuboctahedron’ derives from contraction of the vector equilibrium (cuboctahedron) into the icosahedral form, followed by the octahedron.
STRUTS AND CABLES
 In describing simple models, tensioned elements are often called cables, and compression elements are struts, but the distinctions between ‘cables’ and ‘struts’ can be relative. One of the simplest models is the T-icosa, six compression struts suspended between twenty-four tension cables (strings), with nodes of attachment closely matching (but not quite) the vertices of an icosahedron (it is actually quicker to make it with just a single string).
In describing simple models, tensioned elements are often called cables, and compression elements are struts, but the distinctions between ‘cables’ and ‘struts’ can be relative. One of the simplest models is the T-icosa, six compression struts suspended between twenty-four tension cables (strings), with nodes of attachment closely matching (but not quite) the vertices of an icosahedron (it is actually quicker to make it with just a single string).
In the model shown, two T-icosa’s of different size are joined together by replacing the strut from the model on the right (red dotted) by a cable from the model on the left, which now pulls the nodes of the ‘strut’ apart. We now have an apparent paradox because it is still a cable with respect to the left model but continues to behave like a strut as far as the right model is concerned. It could be said that the entire [left] model has taken the place of the [right] strut, or the entire [right] model the place of the [left] cable, but they have actually become united into a different tensegrity configuration as part of a simple heterarchy. So how is this relevant to biotensegrity?
The Fascia
Originally considered as mere packing tissue, fascia is now recognized to play an important structural role because of its heterarchical nature, and tensional continuity with the extra-cellular matrixGuimberteau and interstitium that surrounds virtually every cell in the body. The multi-level space-filling compartments (bones, muscles, organs etc) within then provide the volume, form and counter-balancing compression of the biotensegrity configuration.
Tension and compression are dependent on each other and always act together – they are what define tensegrity. The smaller compartments thus ‘contain’ proteoglycans (ground-substance) and cells, and contribute to the higher-level space-filling compartments that we refer to as muscles, bones and organs etc.
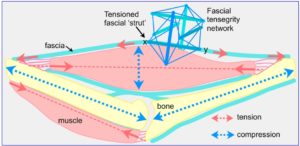 Muscles (higher level) are thus ‘cables’ that generate axial tension, while the resulting changes in the width of their particular fascial compartment also makes them variable length compression struts perpendicular to this; and the same principle applies throughout the body. Bones are ‘struts’ in both length and width that enable the muscles to pull against; and both should be considered as regional specializations of fascia.
Muscles (higher level) are thus ‘cables’ that generate axial tension, while the resulting changes in the width of their particular fascial compartment also makes them variable length compression struts perpendicular to this; and the same principle applies throughout the body. Bones are ‘struts’ in both length and width that enable the muscles to pull against; and both should be considered as regional specializations of fascia.
The definition of cables and struts in a biological context has thus been extended considerably. Any particular piece of a tensegrity structure might be a cable and strut at the same time, depending on how it is considered within the heterarchy, or change emphasis from one to the other throughout movement. Each part may be affected by multiple tensional or compressional influences, but these will ultimately resolve into one or the other at any particular point in space and moment in time. In a sense the difference between what we call ‘cables’ and ‘struts’ is just relative, a useful way of functionally distinguishing between components, but it has its limitations.
 In this modular model of multiple T-icosa, every cable is under tension and every strut under compression, but the whole structure can be stretched to form a cable (tension) or compressed to form a strut, and each of these could be part of other levels in the heterarchy of a larger structure, and so on. In a biological context, the stability of any particular part is likely to depend on a huge number and variety of smaller components, each one with specific material properties that affect how it responds to tension and compression; and these will then influence the mechanical properties of other components at different levels in the heterarchy.
In this modular model of multiple T-icosa, every cable is under tension and every strut under compression, but the whole structure can be stretched to form a cable (tension) or compressed to form a strut, and each of these could be part of other levels in the heterarchy of a larger structure, and so on. In a biological context, the stability of any particular part is likely to depend on a huge number and variety of smaller components, each one with specific material properties that affect how it responds to tension and compression; and these will then influence the mechanical properties of other components at different levels in the heterarchy.
Tension and compression can also be described in various ways that depend on how and where they are being considered.
TENSION AND COMPRESSION
Tension and compression are essentially physical ‘forces’ that are transmitted, or flow, through a particular structure. In simple models, tensioned cables pull on the ends of the compression struts and try to shorten them, while the struts resist the pull of the cables and hold the cable ends apart, and the forces within automatically balance in a state of minimal energy.
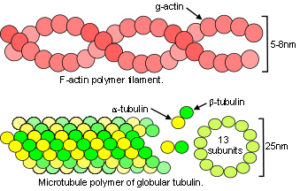 At the most basic level, atoms interact with each other through attraction and repulsion, and spontaneously organize them selves into the most stable and energy-efficient configurations to form crystals and flexible molecules. Connelly; Edwards They do so because of those inter-related principles of geodesic geometry, close-packing and minimal-energy (see geodesics page). Of course, real life is more complicated than that and there many ways in which they can interact with each other, such as van der Waal’s forces that can both attract and repel, depending on the relative position of atoms or a change in pH. Ionic and covalent bonds attract and maintain fixed distances apart that depends on the atoms involved; hydrogen bonds attract but are a bit flexible in spacing; and then there is steric repulsion that maintains a separation between them. ‘Attraction’ and ‘repulsion’ are thus summaries of these different interactions and are the best terms to use at the nano scale, although the same principles operate at every level. ‘Tension’ and ‘compression’ are most appropriate at higher size-scales.
At the most basic level, atoms interact with each other through attraction and repulsion, and spontaneously organize them selves into the most stable and energy-efficient configurations to form crystals and flexible molecules. Connelly; Edwards They do so because of those inter-related principles of geodesic geometry, close-packing and minimal-energy (see geodesics page). Of course, real life is more complicated than that and there many ways in which they can interact with each other, such as van der Waal’s forces that can both attract and repel, depending on the relative position of atoms or a change in pH. Ionic and covalent bonds attract and maintain fixed distances apart that depends on the atoms involved; hydrogen bonds attract but are a bit flexible in spacing; and then there is steric repulsion that maintains a separation between them. ‘Attraction’ and ‘repulsion’ are thus summaries of these different interactions and are the best terms to use at the nano scale, although the same principles operate at every level. ‘Tension’ and ‘compression’ are most appropriate at higher size-scales.
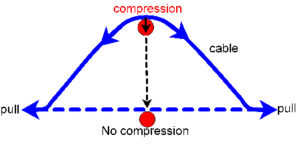 Pull’ (tension) and ‘push’ (compression) are also commonly used terms, and in simple models tensioned cables pull on the nodes and compress the struts, while the struts resist this by ‘pushing’ the nodes apart. Some cables in complex tensegrities could also pull on strut ends and make them longer as part of a functional mechanism regulating strut length. Conversely, the struts could elongate and push on the cables, whose tension now increases, or shorten and become tensioned as the cables try to pull their ends apart. Tension and compression always act in straight lines (at the most basic leve) but can have effects in other directions.
Pull’ (tension) and ‘push’ (compression) are also commonly used terms, and in simple models tensioned cables pull on the nodes and compress the struts, while the struts resist this by ‘pushing’ the nodes apart. Some cables in complex tensegrities could also pull on strut ends and make them longer as part of a functional mechanism regulating strut length. Conversely, the struts could elongate and push on the cables, whose tension now increases, or shorten and become tensioned as the cables try to pull their ends apart. Tension and compression always act in straight lines (at the most basic leve) but can have effects in other directions.
A floppy cable is not under tension until its ends are pulled apart and it starts to straighten itself. As it does so, the middle of the cable pushes to the side (perpendicular compression) anything that might be in its way, ceasing this when it becomes straight. Similarly, the orientation and angles of all the tension cables pulling on a node contributes to the resultant compressional force pushing into the strut (‘parallelogram of forces’ in mechanics terminology), and in a balanced tensegrity structure this is always an axial load. A tension vector thus leads to a compression one when there is a change in angle, and vice versa, and more tension means more compression. Interestingly, a tensioned structure will generally tend to get thinner in the middle, ie. at 90o (‘convergent compression’) while a compressed one bulges (‘divergent tension’) – ‘positive’ Poisson ratio. The T-icosa and many biological tissues demonstrate the opposite and display auxetic behaviour – a ‘negative’ Poisson Ratio.Alderson
 In the cytoskeleton, microtubule length increases in response to a pull from the extracellular matrix, while actomyosin ‘motors’ are able to modulate this by increasing actin tension and maintain a dynamic balance, or generate tension that itself pulls on the matrix. Cellular growth may generate a push on surrounding cells/tissues, and an increase in muscle diameter (on muscle contraction) pushes on associated tissues. Blechschmidt described how tension and compression influence tissue development as a consequence of unequal growth. He reasoned that cartilage develops in regions of dense mesenchyme through a push (compression) from surrounding cells, and an increase in osmotic pressure. Constrained cells then differentiate into chondrocytes, and align in a longitudinal arrangement that pulls on surrounding mesenchyme and leads to muscle formation. Blechschmidt was unaware of the molecular and cytoskeletal interactions that have overshadowed his findings in recent years,Stamenovic; but such mechanical effects have been confirmed to influence morphogenesis and are worth paying attention to.Radlanski
In the cytoskeleton, microtubule length increases in response to a pull from the extracellular matrix, while actomyosin ‘motors’ are able to modulate this by increasing actin tension and maintain a dynamic balance, or generate tension that itself pulls on the matrix. Cellular growth may generate a push on surrounding cells/tissues, and an increase in muscle diameter (on muscle contraction) pushes on associated tissues. Blechschmidt described how tension and compression influence tissue development as a consequence of unequal growth. He reasoned that cartilage develops in regions of dense mesenchyme through a push (compression) from surrounding cells, and an increase in osmotic pressure. Constrained cells then differentiate into chondrocytes, and align in a longitudinal arrangement that pulls on surrounding mesenchyme and leads to muscle formation. Blechschmidt was unaware of the molecular and cytoskeletal interactions that have overshadowed his findings in recent years,Stamenovic; but such mechanical effects have been confirmed to influence morphogenesis and are worth paying attention to.Radlanski
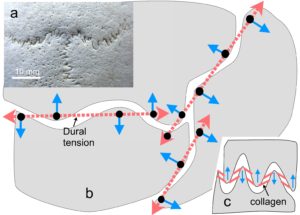
In the tensegrity model of the cranial vault, tensions in the dural membrane and sutural collagen have the effect of pushing the skull bones (compression) apart (~ 100 microns) because of the particular combination of curves in 3-D around the edges of the bones. The bones remain distinct, or as Fuller described it: in “discontinuous compression” (see biology page).
CONTINUOUS TENSION AND DISCONTINUOUS COMPRESSION
Standard anatomy and biomechanic texts take it for granted that bones must be heavily compressed across their joints, i.e. they behave as a system of levers, but this notion is just a hand-down from descriptions of man-made structures in the Seventeenth Century (Borelli) and now highly contentious. A particular feature of tensegrity models is that their compression elements (struts) do not touch each other at any point, i.e. there are no levers, fixed-fulcrums or bending moments, and the biotensegrity concept considers that bones behave similarly.
Levin observed, during surgery, that normal bones do not compress each other in living subjects, and that the knee cartilages are too soft to withstand much compression in any case. This would imply that bones must be held apart by soft tissues, and although the anatomical details that would enable this have largely remained unresolved, biotensegrity explains the basic principles. One of the reasons is the difficulty in modelling complex joint structures at multiple size scales – a feat easily accomplished in biology.
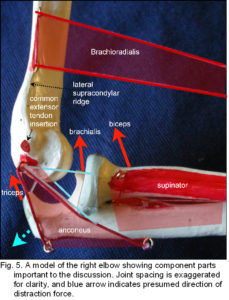 In the elbow, the brachioradialis muscle has a mechanical advantage over other flexors because of its high attachment to the supra-condylar ridge, yet it is reported to be active in rapid and forced flexion, and extension! Rather bizarrely, it is supplied by the same nerve that innervates triceps and anconeus, its supposed ‘antagonists’. When brachioradialis contracts it exerts a distraction force between the bones (blue arrow) that would be contained by triceps, anconeus and the posterior fascia, and it may be that brachioradialis, triceps and anconeus act together as part of a ‘rapid response unit’ that regulates pressure across the joint surfaces (humerus and ulna) and allows them to glide against each other, without being compressed, or even maintain a separation between the bones. Ligaments, capsular and fascial structures then provide the necessary proprioceptive feedback. Cretu mathematically analyzed a tensegrity elbow, confirming the feasibility of this proposal. (See the elbow page)
In the elbow, the brachioradialis muscle has a mechanical advantage over other flexors because of its high attachment to the supra-condylar ridge, yet it is reported to be active in rapid and forced flexion, and extension! Rather bizarrely, it is supplied by the same nerve that innervates triceps and anconeus, its supposed ‘antagonists’. When brachioradialis contracts it exerts a distraction force between the bones (blue arrow) that would be contained by triceps, anconeus and the posterior fascia, and it may be that brachioradialis, triceps and anconeus act together as part of a ‘rapid response unit’ that regulates pressure across the joint surfaces (humerus and ulna) and allows them to glide against each other, without being compressed, or even maintain a separation between the bones. Ligaments, capsular and fascial structures then provide the necessary proprioceptive feedback. Cretu mathematically analyzed a tensegrity elbow, confirming the feasibility of this proposal. (See the elbow page)
Skelton extended tensegrity definitions in engineering applications and divided it into different classes:
Class 1 – compression struts do not touch (conventional tensegrity as defined by Snelson and Fuller).
Class 2 etc – compression struts contact each other at their ends through fixed fulcrums and levers.
This division might be useful in robotic structures but is questionable in a biological context when considering joints from a heterarchical perspective. Engineers are not constrained by the laws of biological organization, natural selection and evolution but by the structural properties of the materials they use, the practicalities of construction and cost, and in a way anything goes. Most man-made structures use materials that are put together in such a way that they can withstand damaging stresses such as shear, torque and bending moments, but also require stronger components to counteract the huge forces generated as they get bigger.
Biological structures have evolved in ways that avoid these stresses by distributing the load amongst smaller components within a heterarchy; if they didn’t, they would be likely to collapse through material fatigue and that would really be the end of them. For example, increasing tension in the extra-cellular matrix causes integrins within associated cell membranes to cluster in ‘focal adhesions’ and distribute the stresses amongst them;Vogel and in bone, a coupled deformation mechanism between collagen and mineral apatite effectively redistributes the strain energy and protects against micro-fractures.Gupta
The separation of tension and compression into different components allows material properties to be optimized, a result of natural physical processes and evolution, and a significant reduction in mass is achieved in a heterarchical biotensegrity arrangement. In the natural world, the most energy-efficient system will always win out, which so far makes tensegrity the most likely candidate in structural evolution. Although biological compression struts can appear to make direct contact with each other at some particular level in the heterarchy, when looked at on a smaller scale they are clearly separate, it is just that the detail of the biotensegrity configuration is not recognized in the first instance; and the knee, elbow and cranial sutures etc are all examples of this. This reasoning goes some way to clarifying Fullers’ assertion that: “everything, properly understood, is a tensegrity structure” and the controversy that followed, which also illustrates the point in biology.Fuller sec 794.00
GEODESIC DOME OR TENSEGRITY
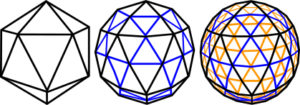 The shape of a geodesic dome is based on a high-frequency icosahedron, a shape that encloses the largest volume within a given surface area of any regular structure apart from a sphere; subdividing each of its triangular faces into smaller triangles produces a higher order, or frequency (1st,2nd and 4th shown here). A sphere is the simplest of all shapes and any point on its surface is equidistant from the centre, just like the vertices of the icosahedron that it can surround; so a line drawn from the centre through each new vertex will project it onto the surface of that sphere. Each higher order of the icosahedron now gets closer to matching the sphere, and because each point is equidistant from all its neighbours, Fuller termed it the geodesic dome. Although the lines now appear to be curved, when looked at closely they are still lots of straight lines.
The shape of a geodesic dome is based on a high-frequency icosahedron, a shape that encloses the largest volume within a given surface area of any regular structure apart from a sphere; subdividing each of its triangular faces into smaller triangles produces a higher order, or frequency (1st,2nd and 4th shown here). A sphere is the simplest of all shapes and any point on its surface is equidistant from the centre, just like the vertices of the icosahedron that it can surround; so a line drawn from the centre through each new vertex will project it onto the surface of that sphere. Each higher order of the icosahedron now gets closer to matching the sphere, and because each point is equidistant from all its neighbours, Fuller termed it the geodesic dome. Although the lines now appear to be curved, when looked at closely they are still lots of straight lines.
A geodesic dome remains stable because of its configuration of triangulated struts; and it is ‘obviously’ not a tensegrity. However, if its constituent atoms and molecules are considered as such, as was described earlier, then it must be a tensegrity at the smaller scale but not at the larger – another of those apparent paradoxes with a difference that depends only on the perspective. Although this would literally mean that everything is a tensegrity, the important point that this example illustrates is that things can appear differently at each level in a heterarchy.
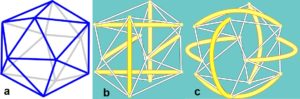
 In the construction of a geodesic dome and tensegrity-icosahedron, each strut and/or cable could be made from a series of similar domes or tensegrities, themselves made from smaller shapes within a self-similar heterarchy.Fuller sec.740.20; Levin The models show a geodesic dome with one strut replaced by a chain of T-icosa, and one with an enlarged vertex beside it. Because the geodesic dome and T-icosa can coexist within each other on the same and multiple levels, so the geodesic dome could become a tensegrity when looked at under a microscope, and the only thing to change would be the size scale. The same can be said for biological heterarchies such as the knee and elbow joints, where what appear to be simple hinges at the macro level are likely to be complex tensegrity configurations at multiple levels below this.
In the construction of a geodesic dome and tensegrity-icosahedron, each strut and/or cable could be made from a series of similar domes or tensegrities, themselves made from smaller shapes within a self-similar heterarchy.Fuller sec.740.20; Levin The models show a geodesic dome with one strut replaced by a chain of T-icosa, and one with an enlarged vertex beside it. Because the geodesic dome and T-icosa can coexist within each other on the same and multiple levels, so the geodesic dome could become a tensegrity when looked at under a microscope, and the only thing to change would be the size scale. The same can be said for biological heterarchies such as the knee and elbow joints, where what appear to be simple hinges at the macro level are likely to be complex tensegrity configurations at multiple levels below this.
STRAIGHT OR CURVED STRUTS
 One of the principles of geodesic geometry is that two points connect together over a straight line, and in 3-D Euclidean space this is always the shortest path, but as this is just one of three geometries that describe 3-D space, the others being ‘spherical’ and ‘hyperbolic’,Terrones; Bowick things are not always this clear cut. Curves are common in biology and it is useful to make models with curved-struts that are compatible with this because they represent multiple levels of complexity.
One of the principles of geodesic geometry is that two points connect together over a straight line, and in 3-D Euclidean space this is always the shortest path, but as this is just one of three geometries that describe 3-D space, the others being ‘spherical’ and ‘hyperbolic’,Terrones; Bowick things are not always this clear cut. Curves are common in biology and it is useful to make models with curved-struts that are compatible with this because they represent multiple levels of complexity.
Tensegrity structures can assume virtually any shape with the forces of tension and compression separated into ‘cables’ and ‘struts’. Because tension acts in a straight line and always tries to reduce itself to a minimum, it causes the ‘cables’ to straighten along the direction of the tensional line. A tensioned structure that is unable to straighten will create shear stresses that potentially lead to a fracture, while a compressed structure will tend to buckle or bend into a curve if the load gets above a certain limit, and this might also fracture. In spite of this, curvature is a means of minimizing energy,Terrones an important consideration in a biological structure, where constituent parts automatically arrange themselves according to the huge complexity of forces acting on them and changes in cell function.
 A sphere is the simplest of all shapes and can surround each of the regular (platonic) and semi-regular shapes so that every vertex touches its surface and is equidistant from the centre. A line connecting each vertex now forms a curve on the surface and divides it into equal parts, the ‘geodesic geometry of a sphere’. Each polyhedral edge follows the line of one of the ‘Great Circles’, equatorial lines described on the sphere that surround all the polyhedral axes of symmetry, and the shortest distance between any two points is now a curve. The sphere thus unites the straight lines of the platonic solids (Euclidean geometry) with the curves of spherical geometry, and together they can be used to understand curvature in biology, certain tensegrity models, and transformations in energy. In the real world, curves are not continuous but made up of lots of geodesic lines at the atomic/molecular scale that lead to the appearance of curves at a higher scale.
A sphere is the simplest of all shapes and can surround each of the regular (platonic) and semi-regular shapes so that every vertex touches its surface and is equidistant from the centre. A line connecting each vertex now forms a curve on the surface and divides it into equal parts, the ‘geodesic geometry of a sphere’. Each polyhedral edge follows the line of one of the ‘Great Circles’, equatorial lines described on the sphere that surround all the polyhedral axes of symmetry, and the shortest distance between any two points is now a curve. The sphere thus unites the straight lines of the platonic solids (Euclidean geometry) with the curves of spherical geometry, and together they can be used to understand curvature in biology, certain tensegrity models, and transformations in energy. In the real world, curves are not continuous but made up of lots of geodesic lines at the atomic/molecular scale that lead to the appearance of curves at a higher scale.
Curved-struts are upper-level representations of heterarchies, and the forces within them, as expressed through spherical geometry at a higher level of complexity (see geodesics page). They only remain stable if their sub-structures are strong enough to resist buckling, or they are part of a biotensegrity configuration that eliminates damaging shear stresses by its very nature.  Although curves can appear at one or many levels in a complex structure, they must contain components that handle tension and compression in straight lines at some smaller scale in order to remain stable. Here a 2-curved-strut model is shown with its modular heterarchical equivalent of struts made from T-icosa joined together. The overall appearance is of curves, but tension and compression are still acting in straight lines as cables and struts at a lower level, and it is the tensegrity configuration that provides the flexibility in shape but without the shear-stresses .
Although curves can appear at one or many levels in a complex structure, they must contain components that handle tension and compression in straight lines at some smaller scale in order to remain stable. Here a 2-curved-strut model is shown with its modular heterarchical equivalent of struts made from T-icosa joined together. The overall appearance is of curves, but tension and compression are still acting in straight lines as cables and struts at a lower level, and it is the tensegrity configuration that provides the flexibility in shape but without the shear-stresses .
Microtubules can appear to buckle and curve but they are functionally balanced by intermediate filaments in what is a tensegrity configuration;Brangwynne curved bones in the skull are at the top of a heterarchy that consists of up to twelve different structural levels, etc etc.
Levin introduced the term biotensegrity to describe tensegrity in living systems, and the definitions of Snelson and Fuller are still applicable to this; the basic principles will always apply no matter what names we use to describe them. The biotensegrity concept is a description of nature’s structural/architectural system and is different from the artificial tensegrities (and limitations) of man-made structures (even though we use the simple stick-and-string models to help understand it).
Some of the examples on these pages may seem to stretch the original definitions but I have tried to reconcile them. Biology generates some interesting quirks and brain-teazers when trying to get to grips with what it is all about. Good definitions should be able to adapt to this by integrating and evolving whilst at the same time maintaining the essence of the subject.
