Geodesics
CONTENTS: platonic solids; helix; tensegrity; curvature; icosahedron and viruses; quasi-crystals; close-packing etc.

 Nature always finds the most energy-efficient way of doing things and that includes geodesic geometry – the connection of points over a straight line (and what is often the shortest distance) and the closest packing of objects together. Geodesic geometry provides the most economic utilization of space and materials and confers strength. It is basic stuff that leads directly into the many different types of close-packing, and is at the heart of tensegrity, with many easily-recognized examples in biology. Geodesic geometry, close-packing and energy-efficiency are the keys to understanding the biotensegrity concept, but remember, we are essentially looking at the vastness of biology so don’t get bogged down in the detail, it is there to stimulate ideas for those who want to go deeper.
Nature always finds the most energy-efficient way of doing things and that includes geodesic geometry – the connection of points over a straight line (and what is often the shortest distance) and the closest packing of objects together. Geodesic geometry provides the most economic utilization of space and materials and confers strength. It is basic stuff that leads directly into the many different types of close-packing, and is at the heart of tensegrity, with many easily-recognized examples in biology. Geodesic geometry, close-packing and energy-efficiency are the keys to understanding the biotensegrity concept, but remember, we are essentially looking at the vastness of biology so don’t get bogged down in the detail, it is there to stimulate ideas for those who want to go deeper.
One of the difficulties with exploring the biotensegrity concept is in knowing where to start, because everything relates to everything else, which is why these pages contain a lot of repetition. The descriptions may seem rather simplistic in places, or even rather complicated, but when taken as a whole will hopefully start to come together. Obtaining and playing with your own set of magnetic bars and ball bearings (e.g. Geomag) is the best way to make all this real, although you could also start with raisins and cocktail sticks.
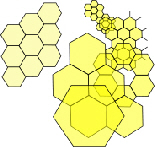
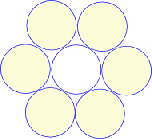
 In two-dimensions, a circle encloses the largest area within the minimum boundary, which makes it a minimal-energy structure, but putting lots of circles next to each other leaves gaps in between that reduce that space-filling efficiency. However, joining the centres of those circles with straight lines (geodesics) creates stable triangles and allows the hexagon to emerge. The best compromise between efficient space-filling of the circle and stability is the triangulated hexagon, with objects of similar size close-packing together to form stable configurations that fill 2-D space completely (tesselation). (The same principle also applies to objects of different sizes.)
In two-dimensions, a circle encloses the largest area within the minimum boundary, which makes it a minimal-energy structure, but putting lots of circles next to each other leaves gaps in between that reduce that space-filling efficiency. However, joining the centres of those circles with straight lines (geodesics) creates stable triangles and allows the hexagon to emerge. The best compromise between efficient space-filling of the circle and stability is the triangulated hexagon, with objects of similar size close-packing together to form stable configurations that fill 2-D space completely (tesselation). (The same principle also applies to objects of different sizes.)
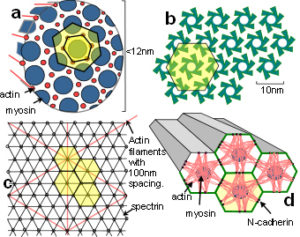
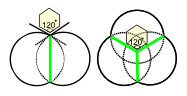
Lots of hexagons support each other at their 3-way junctions but they are only fully stable when triangulated. Hexagons close-pack in an array that can self-generate to produce the same shapes at different size scales and even non-uniform shapes approximate to hexagons as they pack together in sheets. Soap bubbles spontaneously join together with outside surfaces that meet at 120o just like hexagons. This is because soap molecules hold together through their surface tension which tries to minimize itself and reduce the surface area. Cells that are compressed by surrounding tissues and/or pulled together by cadherins tend to predominatly form hexagonal patterns (with a few 5 and 7-sided). This triangulated and hexagonal packing arrangement is also found in (a) muscle fibrils;Kessel (b) the uroplakin complex covering the epithelial lining of the urinary bladder;Sanner (c) the cortical cytoskeleton;Weinbaum (d) the optic lensBassnett and the micro-structure of the avian lung.Maina Close-packing in three-dimensions produces some new shapes called platonic solids that will lead us into biotensegrity.
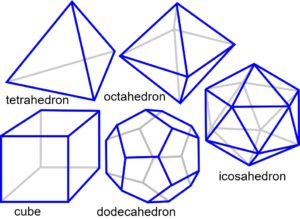 THE PLATONIC SOLIDS
THE PLATONIC SOLIDS
The ancient Greeks considered that just five shapes could describe everything in the universe because they were pure and perfect; and they are the basis for understanding more complex forms in biology. The platonic solids naturally form in 3-D through the efficiencies of geodesic close-packing and principles of symmetry.
Three spheres pack together to form a triangle and four spheres as a tetrahedron. Adding more spheres allows other shapes to emerge because of the similar packing arrangement. The outer faces of each one are all the same with just 3, 4 or 5 sides and each vertex is formed from 3, 4 or 5 faces. The models shown here are made from ping-pong balls, or ball bearings joined with magnetic sticks; the magnets represent the energy bonds that join them into a lattice and may include both attraction and repulsion.

 The Tetrahedron – The tetrahedron packs four spheres into the smallest volume of unit space with the maximum surface area. It also polymerises into a helix that is the basis for secondary protein structure. It is found as methane and water molecules,chaplin the mineral tetrahedrite, a pile of oranges and grains of sand, trabecular bone, honeycomb, and four cells in the early embryo. Adding more spheres forms the second-frequency (2F, order) tetrahedron and leads to the emergence of the octahedron (yellow).
The Tetrahedron – The tetrahedron packs four spheres into the smallest volume of unit space with the maximum surface area. It also polymerises into a helix that is the basis for secondary protein structure. It is found as methane and water molecules,chaplin the mineral tetrahedrite, a pile of oranges and grains of sand, trabecular bone, honeycomb, and four cells in the early embryo. Adding more spheres forms the second-frequency (2F, order) tetrahedron and leads to the emergence of the octahedron (yellow).

 The Octahedron – naturally found in radiolarian structures, the minerals fluorite, diamond and spinel, and the basis of the octet truss used by structural engineers because of its stability. It has 3 equatorial squares at 90o to each other but their stability is maintained because of the triangles at each vertex.
The Octahedron – naturally found in radiolarian structures, the minerals fluorite, diamond and spinel, and the basis of the octet truss used by structural engineers because of its stability. It has 3 equatorial squares at 90o to each other but their stability is maintained because of the triangles at each vertex.
The Cube – forget the familiar 6-sided man-made ‘cubes’ with their 90o angles because this is not how they are constructed in the natural world – we thus have to look at cubes in a different way. Adding a tetrahedron to each of the corners of a 2F-cuboctahedron forms a cube. Removing two corner layers reveals the side of a 4F-tetrahedron (green) and removing a further layer reveals a hexagon ie. all these shapes are contained within each other. The cube is the dual of the octahedron and is naturally found in the minerals galena, pyrite and fluorite. The pictures show that these cube edges appear as zig-zags because of their 60o angles – a much more efficient way of packing objects of similar size together than those with 90o.

 All these shapes occur as mineral crystals with what is traditionally (but unhelpfully for us) called ‘cubic’ symmetry, and because the basic close-packing structure is the same in the tetrahedron, octahedron, cube and cuboctahedron, the same mineral often appears in these different shapes Fuller
All these shapes occur as mineral crystals with what is traditionally (but unhelpfully for us) called ‘cubic’ symmetry, and because the basic close-packing structure is the same in the tetrahedron, octahedron, cube and cuboctahedron, the same mineral often appears in these different shapes Fuller
(The cuboctahedron) Increasing the tetrahedron to its 4th frequency produces the first close packing of 12 spheres around a central nucleus and the emergence of the cuboctahedron (a semi-regular polyhedron but not a platonic solid). This shape is also contained within a 2F-octahedron (see chart) and becomes important when considering biotensegrity from an energetic perspective. This includes the vector equilibrium and jitterbug that will be added in the near future.
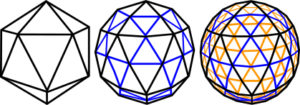
 The Icosahedron
The Icosahedron
By removing the nucleus of the cuboctahedron, 12 spheres can close-pack tighter and at a lower energy level to form an icosahedron. The icosahedron encloses a greater volume for a given surface area than any other type of regular structure apart from a sphere, which makes it materially efficient; triangulation makes it very stable with its 12 vertices, 20 triangular faces and 30 edges. It demonstrates multiple symmetries (also cubic), six 5-fold, ten 3-fold and fifteen 2-fold which allow it to polymerize in a thick planar sheet, form rods, helixes and branching structures, and as a fractal generator create more complex patterns and shapes at multiple size scales. The icosahedron is different to the other platonic shapes because the addition of more spheres to the outside will not create higher orders or frequencies as they won’t all touch. A 2nd frequency icosahedron won’t close-pack around the basic shape, or a 3F around a 2F, because they would be unstable. It can only exist in its own right as a single outer shell and enlarges by subdividing each of its faces into more triangles. Some naturally  occurring structures based on the icosahedron are carbon fullerenes (‘Buckyballs’),Terrones radiolaria, pollen grains, ‘spherical’ virusescaspar and clathrins (endocytic vesicles beneath the cell membrane). The icosahedron is also a fundamental pattern in the structure of quasi-crystals, a relatively new field of study in the crystalline structure of metals, waterchaplin and organic moleculessadoc (more details later). Levin has proposed the icosahedron as the finite-element of biological structure.levin
occurring structures based on the icosahedron are carbon fullerenes (‘Buckyballs’),Terrones radiolaria, pollen grains, ‘spherical’ virusescaspar and clathrins (endocytic vesicles beneath the cell membrane). The icosahedron is also a fundamental pattern in the structure of quasi-crystals, a relatively new field of study in the crystalline structure of metals, waterchaplin and organic moleculessadoc (more details later). Levin has proposed the icosahedron as the finite-element of biological structure.levin
The (pentagonal) dodecahedron
This dodecahedron is the dual of the icosahedron and is found in pollen grains and the central core of some proteins structures;Izard it is also involved in water and quasi-crystal structures. It is included here for the sake of completeness but doesn’t get a lot of attention here.

 THE HELIX
THE HELIX
At a basic level, four spheres close-pack together as a tetrahedron and occupy the smallest proportion of unit space within the largest surface area.Sadoc The addition of more spheres as in the lattice packing of the tetrahedron, octahedron and cube increases that proportion because of the squares within the octahedra but the tetrahelix, a tetrahedral polymer, comes closer to the minimum making it a more suitable model for molecular packing because of this margin of energy-efficiency. The tetrahelix also displays inherent hierarchy with its sub-helixes of different chirality and pitch. Mapping a tetrahelix onto a plane surface by ‘unzipping’ one of its long helical edges displays the packing efficiency of the triangular pattern as described earlier.  Rolling that map into a cylinder demonstrates equivalence, a property important to secondary protein structures, as described below and on the biology page.Caspar Equi-valence implies a symmetrical balance of forces and the only shapes that can accommodate it have surfaces based on the platonic solids and cylinders.
Rolling that map into a cylinder demonstrates equivalence, a property important to secondary protein structures, as described below and on the biology page.Caspar Equi-valence implies a symmetrical balance of forces and the only shapes that can accommodate it have surfaces based on the platonic solids and cylinders.
Equivalence restricts the number of possible structures but evolution has evaded this constraint through ‘quasi-equivalence’, where structural proteins can contort slightly in order to conform to the ‘ideal’ geodesic template. Interestingly the central space within a tropocollagen molecule is a tetrahelix; the three chains of procollagen each contain a glycine at every third position, and a hydrogen atom on each one of these corresponds to one of the spheres in the picture.Sadoc The tetrahelix is the geometric basis for helical molecules and a model for coiled winding in many biological structures.
 Flower heads display well recognized patterns of spirals (parastichies) that run in opposite directions, a result of the most efficient close-packing arrangement of objects of changing size in the tips of growing plants. The number of elements within each opposing spiral is nearly always two consecutive numbers of the Fibonacci sequence where each new term is the sum of the two preceding ones (1,1,2,3,5,8,13,21,34…). The ratio of any two consecutive numbers approximates to the Golden Mean (1.61804) and becomes closer as the sequence gets higher.Douady The helical pattern on the side of a pineapple, arrangement of branches on a plant stem, microtubules,Hameroff coronary artery lesionsGibson and tropocollagen packingCharvolin relate to the same generative sequence. The Golden Mean often appears in the proportions of biological structures and platonic solids. Have a look at Vi Harts summary videos. vid 1; vid 2; vid 3
Flower heads display well recognized patterns of spirals (parastichies) that run in opposite directions, a result of the most efficient close-packing arrangement of objects of changing size in the tips of growing plants. The number of elements within each opposing spiral is nearly always two consecutive numbers of the Fibonacci sequence where each new term is the sum of the two preceding ones (1,1,2,3,5,8,13,21,34…). The ratio of any two consecutive numbers approximates to the Golden Mean (1.61804) and becomes closer as the sequence gets higher.Douady The helical pattern on the side of a pineapple, arrangement of branches on a plant stem, microtubules,Hameroff coronary artery lesionsGibson and tropocollagen packingCharvolin relate to the same generative sequence. The Golden Mean often appears in the proportions of biological structures and platonic solids. Have a look at Vi Harts summary videos. vid 1; vid 2; vid 3
TENSEGRITY

 The platonic solids are fundamental to understanding tensegrity and biological structure because of their geodesic geometry, close-packing and minimal-energy efficiency. A simple tensegrity model consists of a set of struts under compression and an arrangement of cables under tension; it is a geodesic structure by its very nature because tension always acts in straight lines and automatically tries to reduce itself to a minimum.Pars It is a close-packed structure because each resting part is as close as it can get to the others, and it naturally settles into the most energy-efficient configurataion.
The platonic solids are fundamental to understanding tensegrity and biological structure because of their geodesic geometry, close-packing and minimal-energy efficiency. A simple tensegrity model consists of a set of struts under compression and an arrangement of cables under tension; it is a geodesic structure by its very nature because tension always acts in straight lines and automatically tries to reduce itself to a minimum.Pars It is a close-packed structure because each resting part is as close as it can get to the others, and it naturally settles into the most energy-efficient configurataion.
The resultant pull of the cables is automatically balanced by the struts, which remain distinct and do not touch each other at any point, with the cables providing structural integrity so that the compression elements appear to float within the tensioned network. Because each component influences all the others, stresses are distributed throughout the system creating a structure that can react to external forces from any direction without collapsing. An infinite variety of stable and complex shapes thus become possible by changing the lengths and numbers of struts, with changes in shape that can be accomplished with very little control energy.Skelton Because atoms attract (~tension) and repel (~compression) each other to form crystals and molecules they must inherently be tensegrities.Connelly; Zanotti Tensegrity structures also display non-linear mechanical propertiesKenner p16; Motro p127 just like biological structures; and an organism utilizing such a system would be able to move with the minimum of energy expenditure without losing stiffness or stability. Because tension and compressional forces are separated, the material properties of each component can be optimized, and in biological systems this typically occurs through heterarchies (see biology and definitions pages); even the cables and struts are made from smaller components, as shown in this ‘enlarged’ example of a node (strut-cable connections), and shear stresses are eliminated. Potentially damaging stresses are thus transferred down to a lower level where they ultimately balance in the attraction and repulsion between molecules.

 The simplest tensegrity model is made from three struts and forms the start of an infinite series of cylindrical structuresPugh that have a left or right-handed twist between their polygonal ends (chirality) referred to as the T3-prism (simplex/triplex), T4-prism (quadruplex) and T5-prism (pentaplex) etc; polymers of these structures are called T-helixes.
The simplest tensegrity model is made from three struts and forms the start of an infinite series of cylindrical structuresPugh that have a left or right-handed twist between their polygonal ends (chirality) referred to as the T3-prism (simplex/triplex), T4-prism (quadruplex) and T5-prism (pentaplex) etc; polymers of these structures are called T-helixes.
The twist conforms to the formula: angle of twist = 90o – 180o/n where n equals the number of struts; thus the T3-prism has a twist of 30o between the upper and lower ends and 45o for the T4-prism.
Stable nano-structures of DNA based on the T3-prism and platonic solids can spontaneously assemble in-vitro.liedl Interestingly, only 0.4% of helical proteins are left-handed but left-handed procollagen contributes to the most widespread of all proteins – collagen.Novotny
T-prisms can be polymerized into a regular stacking of individual components (T-helixes) and more complex shapes that compare with those found in biology. Increasing the number of struts causes their centres to position more towards the outside of the structure, enlarging the central space, and eventually forming a tubular ‘wall’ due to the changing orientation. Because each strut could be made from a smaller helix, or the whole structure become part of a strut within a larger helix, it has inherent hierarchical potential with many properties useful to organic life (see helix and myofascial page). This T-helix is four T6-prisms joined together and seen from the end and side.
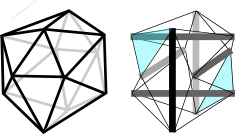 Two T3-prisms of opposite chirality join together to form the T-icosahedron (T-icosa) (Pugh classified this as a ‘spherical’ tensegrity and it is also sometimes referred to as an expanded octahedron and reducing cuboctahedron; see the definitions page for the reasoning). The T-icosa has six compression struts suspended within twenty-four tension cables with nodes of attachment closely matching (but not exactly) the vertices of an icosahedron. The outside of the structure is entirely under tension with the struts acting as an endoskeleton. The six struts can be considered in different groups of three joined on the surface by ‘tension triangles’ (blue). Each strut within the group is oriented at 90o to the others within the group and together they create a chiral twist. On the other side of the structure is a group with an opposite twist. Levin considered the icosahedron to be the finite element of biological structure and it is also very useful for modelling complex shapes.Levin Marcelo Pars is one of the masters of tensegrity models and has discovered alternative configurations for the icosahedron.
Two T3-prisms of opposite chirality join together to form the T-icosahedron (T-icosa) (Pugh classified this as a ‘spherical’ tensegrity and it is also sometimes referred to as an expanded octahedron and reducing cuboctahedron; see the definitions page for the reasoning). The T-icosa has six compression struts suspended within twenty-four tension cables with nodes of attachment closely matching (but not exactly) the vertices of an icosahedron. The outside of the structure is entirely under tension with the struts acting as an endoskeleton. The six struts can be considered in different groups of three joined on the surface by ‘tension triangles’ (blue). Each strut within the group is oriented at 90o to the others within the group and together they create a chiral twist. On the other side of the structure is a group with an opposite twist. Levin considered the icosahedron to be the finite element of biological structure and it is also very useful for modelling complex shapes.Levin Marcelo Pars is one of the masters of tensegrity models and has discovered alternative configurations for the icosahedron.
 MORE ON GEODESIC GEOMETRY
MORE ON GEODESIC GEOMETRY
As described earlier, the complete filling of space in 2-D with a single regular shape (tessellation) can only be accomplished with triangles, squares, rhomboids and hexagons (3, 4 and 6 sides). The resulting pattern is called ‘periodic’, because it repeats itself perfectly when all the tiles are moved a fixed distance in a given direction (translation), and examples of hexagons can be observed in biology.

 The simplest structure in 3-D is a tetrahedron that can be enlarged to produce a close-packing configuration that is also periodic and allows the emergence of other shapes – squares, hexagons, cubes, octahedra and cuboctahedra. These shapes are mostly found in crystal structures but can appear within proteinsIzard;Day and radiolaria. They all have 2, 3, 4 or 6-fold symmetry but 5-fold symmetry can be found in the icosahedron and its dual the dodecahedron.
The simplest structure in 3-D is a tetrahedron that can be enlarged to produce a close-packing configuration that is also periodic and allows the emergence of other shapes – squares, hexagons, cubes, octahedra and cuboctahedra. These shapes are mostly found in crystal structures but can appear within proteinsIzard;Day and radiolaria. They all have 2, 3, 4 or 6-fold symmetry but 5-fold symmetry can be found in the icosahedron and its dual the dodecahedron.
The icosahedron has twelve vertices, twenty triangular faces and thirty edges, and each face can be divided into smaller triangles that are similar (the dodecahedron has twenty vertices and twelve faces).
 All the regular (platonic solids) and semi-regular (cuboctahedron and rhombic dodecahedron) polyhedra have specific numbers of vertices that are equally spaced apart and
All the regular (platonic solids) and semi-regular (cuboctahedron and rhombic dodecahedron) polyhedra have specific numbers of vertices that are equally spaced apart and
connected by straight lines (tetrahedron 4, octahedron 6, cube 8, icosahedron and cuboctahedron 12, and dodecahedron 20). The regular shapes with triangular faces can be subdivided into smaller triangles and create a higher order or ‘frequency’ of that shape, a process that can be continued indefinitely. These shapes are thus termed generators with the number of vertices and triangular intersections at higher frequences forming a sequence that is different for each of the generators.Butcher
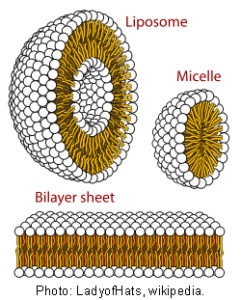
These numbers have been applied to lipid structures such as micelles and membranes. Micelles are formed when certain molecules such as fatty acids and their salts (soap), phospholipids etc. are added to a liquid. In water their long hydrophobic tails are repelled towards the centre and form a helical arrangement while polar heads surround the outside. The number of unit heads that can be arranged more or less evenly around the outside of a sphere may relate to quasi-crystalline packing.Ungar
CURVATURE

 A principle of geodesic geometry is that any two points in 3-dimensional Euclidean space (E3) are connected in a straight line and over the shortest distance. However this is only one of three geometries that describe 3-D space, the others being ‘spherical’ and ‘hyperbolic’.Terrones;Bowick Curves are common in biology and can be a means of minimizing energy, with spherical geometry describing energy-minimizing surfaces such as soap bubbles, cell membranes and liquid interfaces, and curved-strut tensegrity models that are simplifications of more complex hierarchies (see definitions page).
A principle of geodesic geometry is that any two points in 3-dimensional Euclidean space (E3) are connected in a straight line and over the shortest distance. However this is only one of three geometries that describe 3-D space, the others being ‘spherical’ and ‘hyperbolic’.Terrones;Bowick Curves are common in biology and can be a means of minimizing energy, with spherical geometry describing energy-minimizing surfaces such as soap bubbles, cell membranes and liquid interfaces, and curved-strut tensegrity models that are simplifications of more complex hierarchies (see definitions page).
In the real world, curves are not continuous but made up of lots of straight lines (attraction and repulsion ‘forces’ between atoms) that give the appearance of curves at a higher scale, and the high-frequency icosahedron as a minimal-energy structure illustrates this; it encloses the largest volume within a given surface area, of any regular structure apart from a sphere. A sphere can surround each of the regular platonic shapes so that every vertex touches its surface; each triangular face can then be divided into smaller triangles and the points of contact projected onto the surface of that sphere to form new vertexes, so although each one is still connected by a straight line, successive higher orders now get closer to the appearance of a sphere.
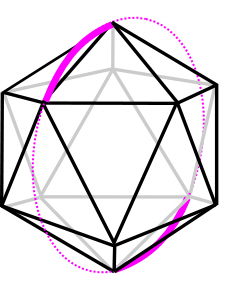
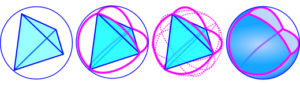 From this higher perspective, the shortest distance between any two points now appears to be a curve, with the vertexes dividing the spherical surface into equal parts. Each polyhedral edge follows the line of one of the ‘Great Circles’, equatorial lines described on the sphere that surround all the polyhedral axes of symmetry, and the diagrams show this with an icosahedron and tetrahedron.fuller A sphere is really a 2-D curved surface (S2) embedded in a 3-D space and it is only from the mathematical perspective and convenience that we describe these lines as curved, because all ‘curves’ in biology are ultimately straight lines at some smaller scale.
From this higher perspective, the shortest distance between any two points now appears to be a curve, with the vertexes dividing the spherical surface into equal parts. Each polyhedral edge follows the line of one of the ‘Great Circles’, equatorial lines described on the sphere that surround all the polyhedral axes of symmetry, and the diagrams show this with an icosahedron and tetrahedron.fuller A sphere is really a 2-D curved surface (S2) embedded in a 3-D space and it is only from the mathematical perspective and convenience that we describe these lines as curved, because all ‘curves’ in biology are ultimately straight lines at some smaller scale.
MORE ON THE ICOSAHEDRON AND VIRUSES
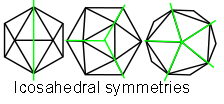 The basic icosahedron has 12 vertices, 20 triangular faces and 30 edges, and like all the platonic solids can be superimposed onto a sphere so that it tesselates the surface into equal parts. It has 15 x 2-fold, 10 x 3-fold and 6 x 5-fold symmetries, and its topology can describe the outer capsid shell structure of many of the ‘spherical’ viruses.Crick; Caspar
The basic icosahedron has 12 vertices, 20 triangular faces and 30 edges, and like all the platonic solids can be superimposed onto a sphere so that it tesselates the surface into equal parts. It has 15 x 2-fold, 10 x 3-fold and 6 x 5-fold symmetries, and its topology can describe the outer capsid shell structure of many of the ‘spherical’ viruses.Crick; Caspar
Dividing a sphere into 20 triangular parts is the most efficient way of pr
oducing a shell with identical components that are all bonded together in the same way, or equivalently (equi-valently), making the icosahedron a minimal-energy structure. Each triangular face can encode the location of three protein subunits in its corners, and because proteins are asymmetrical and unlikely to conform precisely to the icosahedral geometry, they must contort slightly to facilitate bonding.
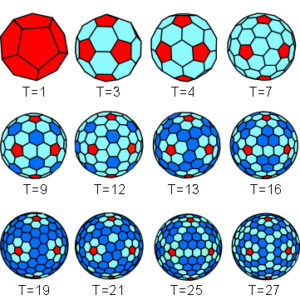
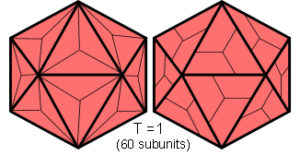
 The icosahedron enlarges by subdividing each of its triangular faces but the maximum number of components that can be joined in an equivalent manner is just 60 (20 x 3-fold symmetry); some viruses have protein capsids constructed of just 60 units and there are several possible arrangements but most have many more. Increasing the number of units beyond this whilst preserving the icosahedral template means that the bonding between them cannot all be the same, because some are joined together to form pentamers, with each vertex surrounded by 5 identical protein subunits, and others as hexamers with 6 protein subunits joining together. Caspar and Klug introduced the theory of quasi-equivalence to take account of this.
The icosahedron enlarges by subdividing each of its triangular faces but the maximum number of components that can be joined in an equivalent manner is just 60 (20 x 3-fold symmetry); some viruses have protein capsids constructed of just 60 units and there are several possible arrangements but most have many more. Increasing the number of units beyond this whilst preserving the icosahedral template means that the bonding between them cannot all be the same, because some are joined together to form pentamers, with each vertex surrounded by 5 identical protein subunits, and others as hexamers with 6 protein subunits joining together. Caspar and Klug introduced the theory of quasi-equivalence to take account of this.
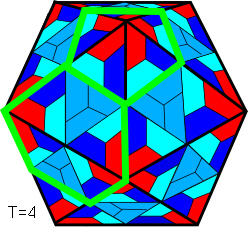
Because the number of subunits in the larger viruses can be quite high, the ‘T-number indicates how many there are within each of the 60 triangular units. So, while a T=1 has all 60 subunits (protein capsomeres) with similar bonding and in equivalent positions, T>1 has some with different arrangements that are called quasi-equivalent. The icosahedral template can thus have 20T structural units that can be clustered as 20T trimers, 30T dimers or 60T monomers. As capsomeres dont necessarily correspond exactly with the triangulated lattice, diagrams frequently simplify things to just show the pentamers and hexamers (superimposed green lines) as Goldberg polyhedra;Goldberg;Zandi;Twarock there will always be at least 12 pentamers but the number of hexamers varies as 10(T-1). The principle of quasi-equivalence has also been found to govern the assembly of pyruvate dehydrogenase complexes with cubic and dodecahedral cores.Izard
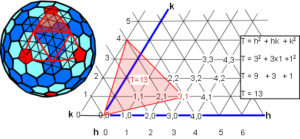
 The T-number can be worked out on a triangulated lattice according to the formula T = h2 + hk + k2 where h and k are the coordinates at 60o; some of these coordinates are shown with the T=13 highlighted in red.
The T-number can be worked out on a triangulated lattice according to the formula T = h2 + hk + k2 where h and k are the coordinates at 60o; some of these coordinates are shown with the T=13 highlighted in red.
Polio virus is T=1, Picorna virus is T=3, Hepatitis B virus is T=3 or 4, Herpes simplex virus is T=16, and Bovine papilloma virus is T=7 and made entirely of pentamers.
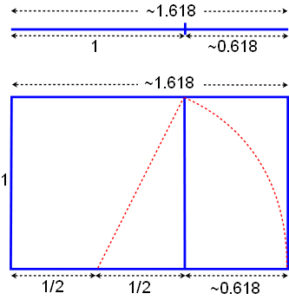
For many years, the capsid proteins of some spherical viruses (papovaviridae) didn’t seem to fit with this icosahedral symmetry, but it is now known that they relate to it through the Fibonacci sequence, Golden Mean and Penrose tiling.Twarock;Keef Consecutive numbers of the Fibonacci series are in a ratio that approximates the Golden Mean and becomes closer as the series gets higher, the diagram shows how it relates to a line and square.Green The golden mean (~ 1.618) is also fundamental to the geometry of five and ten-fold symmetry and is a mathematical irrational constant embedded in the structure that describes a continuous balanced proportionality, it displays itself through Penrose tilings.
PENROSE TILING

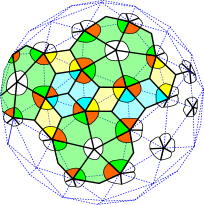
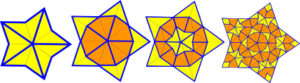 Penrose tilingWiki;Lord uses two or more different shapes to tessellate the 2-D plane (E2) in a pattern that has pentagonal symmetry and is non-periodic, ie it lacks translational symmetry and does not repeat itself completely;Hwang a shifted copy will never match the original exactly. Common shapes are rhomboids, and ‘darts and kites’, which can be superimposed on each other, and their relative numbers and area
Penrose tilingWiki;Lord uses two or more different shapes to tessellate the 2-D plane (E2) in a pattern that has pentagonal symmetry and is non-periodic, ie it lacks translational symmetry and does not repeat itself completely;Hwang a shifted copy will never match the original exactly. Common shapes are rhomboids, and ‘darts and kites’, which can be superimposed on each other, and their relative numbers and area
s are connected to each other through the Golden Mean.
Parts of the pattern do recur at different size scales (self-similarity) so that any finite patch within the tiling is contained somewhere inside every other (local isomorphism) and this hierarchical pattern continues indefinitely through inflation and deflation as a true fractal.Ramachandarao
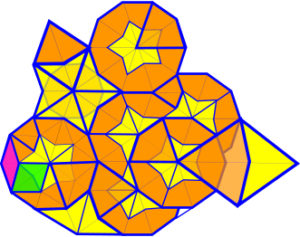
 An analogue of Penrose tiling in 3-D is the icosahedronLevine because of the 5-fold symmetry, and enables those previously unclassified viruses (papovaviridae) to be placed in a geometric system that now includes all the ‘spherical’ viruses.Twarock;Keef Here the coloured capsid proteins are positioned on the nodes of the triangulated lattice but connect to each other as dimers and trimers in a pentagonal symmetry; they are still quasiequivalent. Virus capsids spontaneously self-assemble into these patterns and shapes because they are the most energetically efficient configurations, and this also provides a built-in
An analogue of Penrose tiling in 3-D is the icosahedronLevine because of the 5-fold symmetry, and enables those previously unclassified viruses (papovaviridae) to be placed in a geometric system that now includes all the ‘spherical’ viruses.Twarock;Keef Here the coloured capsid proteins are positioned on the nodes of the triangulated lattice but connect to each other as dimers and trimers in a pentagonal symmetry; they are still quasiequivalent. Virus capsids spontaneously self-assemble into these patterns and shapes because they are the most energetically efficient configurations, and this also provides a built-in
genome release mechanism because of the inhomogeneous stress distribution.
Conventionally, mineral crystals can only have 2,3,4 and 6-fold symmetries with highly ordered arrays of atoms and long-range periodic translational order, but no 5-fold rotational symmetry. The icosahedron has this ‘forbidden’ symmetry, and the Penrose tiling (2-D) and pentagonal arrangement of capsid proteins on viruses relates it to a different class of minimal-energy structures called quasi-crystals.
To ensure that Penrose tiles are arranged non-periodically the edges are matched with specific lines drawn across each tile (Amman bars) and these then reveal a hidden symmetry.
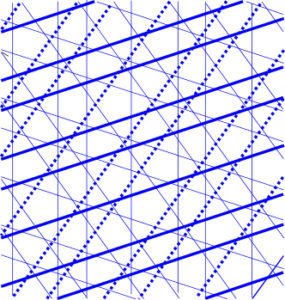

 The bars form five sets of parallel lines spaced in long and short intervals according to numbers in the Fibonacci sequence and oriented normal to the five axes of a regular pentagon. Penrose tilings thus generate patterns that are governed by the Golden Mean and are not just ‘non-periodic’ but also quasi-periodic, due to this underlying long-range order in 1-D.Levine
The bars form five sets of parallel lines spaced in long and short intervals according to numbers in the Fibonacci sequence and oriented normal to the five axes of a regular pentagon. Penrose tilings thus generate patterns that are governed by the Golden Mean and are not just ‘non-periodic’ but also quasi-periodic, due to this underlying long-range order in 1-D.Levine
The Fibonacci sequence is an example of a quasi-periodic pattern that describes a whole new class of minimal-energy structures that can have any symmetry in any number of dimensions and termed quasi-crystals.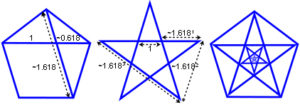 In order to appreciate this multi-dimensional world more fully and relate it to tensegrity we need some examples.
In order to appreciate this multi-dimensional world more fully and relate it to tensegrity we need some examples.
QUASI-CRYSTALS
When we look at a photograph in 2-D (E2) our brains make sense of it by mentally visualizing it in 3-D (E3), because they are used to seeing things in this way, but sometimes several images are needed in order to give a good representation of that object (see cube pictures); these 2-D images are specific projections of objects that exist in 3-D. In the same way, 4-D objects can be projected into 3-D but this time we don’t recognize them as easily because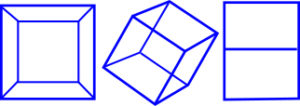 we cannot see this mathematically higher dimension directly. The same can also happen with higher dimensions such as 5-D and 6-D etc.
we cannot see this mathematically higher dimension directly. The same can also happen with higher dimensions such as 5-D and 6-D etc.
Quasi-crystalsquasi are ordered structures that continuously fill space but are non-periodic and lack translational symmetry. Each unit cell has a different configuration of cells surrounding itShectman;Levine and atoms and molecules are not spaced at regular intervals but in ways that relate to each other through the Golden Mean. Quasicrystals can have any symmetry in any number of dimensions, and any quasi-periodic pattern of points can be formed from a periodic pattern in some higher dimension.Ho;Socolar Thus, Penrose tilings as prototype quasi-crystals can be obtained from a regular lattice in 5-D via projection, and those that describe viral capsids can be obtained from a suitable lattice in 6-D, the smallest dimension in which a lattice invariant under the icosahedral group can occur.

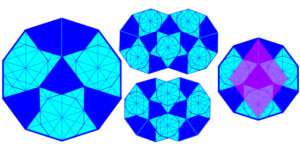 Gummelt found a non-periodic tiling that used a single tile decorated with coloured patches; the decagons are arranged so that similar patches in adjacent decagons overlap (the tiling can also be mapped to a Penrose tiling with the rhombus). The value of this tiling pattern is that it shows that crystals can be built using a single quasi-unit building block in 3-D, with atoms shared by different clusters in the quasi-crystal. Hwang;Wiki;Lord
Gummelt found a non-periodic tiling that used a single tile decorated with coloured patches; the decagons are arranged so that similar patches in adjacent decagons overlap (the tiling can also be mapped to a Penrose tiling with the rhombus). The value of this tiling pattern is that it shows that crystals can be built using a single quasi-unit building block in 3-D, with atoms shared by different clusters in the quasi-crystal. Hwang;Wiki;Lord
Quasi-crystals with icosahedral symmetry are found in some metallic alloysSchectman;Levine;Lord and icosahedral and dodecagonal quasi-crystal phases of water occur under certain conditions.Johnstone Water soluble micelles can assemble into liquid-crystal colloidal structures with quasi-crystalline symmetries (12 and 18)Fischer;Socolar and soft-matter quasicrystals have also been found;Iacovella;Ungar even collagen has been shown to have a quasi-crystalline structure that relates the tetrahedron and icosahedron to the arrangement of atoms in the molecule.Sadoc;Lord This is especially interesting from a tensegrity perspective because if quasi-crystals link the platonic solids with complex molecular structures, which are tensegrities in their own right,Zanotti then this adds support to the importance of simple geometry and tensegrity in even more complex biological structures.
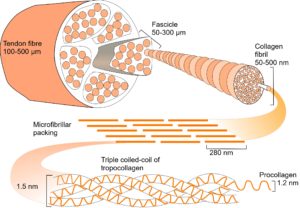
 Collagen is constructed from three left-handed helical chains of amino-acids (procollagen) that wind around each other to form a right-handed triple-helical molecule of tropocollagen. Every third amino-acid in each chain is a glycine, and a hydrogen atom from each one projects into the common centre between the chains and corresponds to a vertex of the right-handed tetrahelical core.
Collagen is constructed from three left-handed helical chains of amino-acids (procollagen) that wind around each other to form a right-handed triple-helical molecule of tropocollagen. Every third amino-acid in each chain is a glycine, and a hydrogen atom from each one projects into the common centre between the chains and corresponds to a vertex of the right-handed tetrahelical core.
The tetrahelix is a close-packed chain of tetrahedra that cannot fill Euclidean space (E3), but can be projected into spherical space (S3) so that 600 tetrahedra pack together and completely fill it, as well as allowing regular icosahedra to emerge;Lord;Sadoc they also wind around a torus to form a closed loop that will take us into hyperbolic geometry. The three procollagen chains (with the tetrahelical core between them) together give rise to a series of slightly distorted icosahedra, but these become regular when projected into S3.
Quasi-crystals illustrate how geometric shapes in one dimension can look different in another, and means that structures that appear to us to be randomly organized in 3-D can become regular and explainable at some higher dimension. Icosahedral symmetries and the Golden Mean commonly occur in plants and it may be that many quasi-crystal symmetries are realized in nature but have not yet been detected.Socolar
HYPERBOLIC GEOMETRY
 To get a bit more technical, the sphere is a 2-D surface embedded in 3-D space, and such surfaces consist of two principle curvatures that can be positive or negative. In Euclidean geometry both curvatures are zero and result in a flat plane and straight lines (E2); in spherical geometry they are both positive (greater than zero) and the surface bends equally on both sides (S2); but in hyperbolic geometry they are positive and negative (less than zero) which can give the surface a saddle shape (H2)(eg. the catenoid in the middle of this torus).Terrones
To get a bit more technical, the sphere is a 2-D surface embedded in 3-D space, and such surfaces consist of two principle curvatures that can be positive or negative. In Euclidean geometry both curvatures are zero and result in a flat plane and straight lines (E2); in spherical geometry they are both positive (greater than zero) and the surface bends equally on both sides (S2); but in hyperbolic geometry they are positive and negative (less than zero) which can give the surface a saddle shape (H2)(eg. the catenoid in the middle of this torus).Terrones
To put this another way, in Euclidean geometry the sum of the internal angles of a triangle is exactly 180o; in spherical geometry it is greater than 180o and in hyperbolic geometry it is less than 180o, because the edges are curved.
 The butterfly outlined in white on the centre of the torus becomes stretched as the inside is rotated up and around to the outside, and contracts before reappearing again at the catenoid centre.
The butterfly outlined in white on the centre of the torus becomes stretched as the inside is rotated up and around to the outside, and contracts before reappearing again at the catenoid centre.
Curves with constant curvature and torsion are helixesChouaieb and cylindrical tensegrities (T-prisms and T-helixes) relate to hyperbolic geometry through the catenoid and torus.Pars
The Poincare disc is another model of hyperbolic geometry that displays patterns with a remarkable similarity to biology.Hart;Nylander
The Klein bottle model is peculiar in that it only has one surface with no clear distinction between inside and outside and relates to the Möebius strip.Wiki It is really a 4-dimensional object that cannot be visualized directly, but a projection looks like one end of the bottle curves around and passes through the wall, before opening out and joining with the ‘inside’ of the other end (in 4-D it is not actually penetrating the surface).
Because a tensegrity structure doesnt have a distinct boundary between inside and outside either it makes a more visually realistic model of the klein bottle and has also been related to embryonic development.Rappoport
MORE ON GEODESIC GEOMETRY – some musings


 There are many consequences of close-packing and they can lead into some interesting shapes with possible relevance to biological structures. The picture on the left shows the 3-D packing arrangement for the tetrahedron (as described earlier), and the one next to it shows an alternative configuration. The tops of the tetrahedra are now closer together and connecting them (yellow) causes the whole structure to bend and form an arch that is also twistable (below).
There are many consequences of close-packing and they can lead into some interesting shapes with possible relevance to biological structures. The picture on the left shows the 3-D packing arrangement for the tetrahedron (as described earlier), and the one next to it shows an alternative configuration. The tops of the tetrahedra are now closer together and connecting them (yellow) causes the whole structure to bend and form an arch that is also twistable (below).


 The addition of more spheres on the top (yellow & red) brings both (curved) sides to an apex, and on the bottom (green & red) to a new pattern with regular spacing. The underside of this structure demonstrates symmetry breaking as it gets larger because the ability of tetrahedrons (and icosahedra) to close-pack and fill 3-D Euclidean space completely is limited. Some more examples of close-packing and how curves can develop are shown here.
The addition of more spheres on the top (yellow & red) brings both (curved) sides to an apex, and on the bottom (green & red) to a new pattern with regular spacing. The underside of this structure demonstrates symmetry breaking as it gets larger because the ability of tetrahedrons (and icosahedra) to close-pack and fill 3-D Euclidean space completely is limited. Some more examples of close-packing and how curves can develop are shown here.

 Atoms have different sizes and can attract or repel each other in different ways, which leads to an enormous variety of possible interactions, although certain configurations predominate. Tetrahedra, octahedra and icosahedra are frequently the basic building blocks in crystals and molecules because of their energically efficient configurations.
Atoms have different sizes and can attract or repel each other in different ways, which leads to an enormous variety of possible interactions, although certain configurations predominate. Tetrahedra, octahedra and icosahedra are frequently the basic building blocks in crystals and molecules because of their energically efficient configurations.
The red connectors in the tetrahedral packings below represent points of symmetry breaking (because the equal-length red connectors cannot attach to the spheres at both ends) and are thus free to form other attachments elsewhere. As all the components close-pack and the structure gets larger, ‘chaotic’ development apparently takes over. The addition of more tetrahedra, octahedra and icosahedra will eventually form what seem completely random and asymmetric shapes even though they have an underlying ‘platonic’ basis. 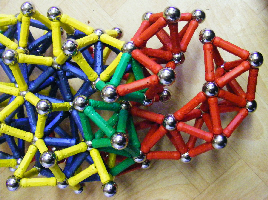

 More components fill the spaces but become limited in the same way and thus different hierarchical levels become apparent. When attractive and repulsive forces cause atoms to spontaneously assemble into the most energetically efficient configurations they are following the same principles that govern the stick and string tensegrity models. Tensegrity seems to be the best explanation of how all these forces and structures link together in a hierarchical manner.
More components fill the spaces but become limited in the same way and thus different hierarchical levels become apparent. When attractive and repulsive forces cause atoms to spontaneously assemble into the most energetically efficient configurations they are following the same principles that govern the stick and string tensegrity models. Tensegrity seems to be the best explanation of how all these forces and structures link together in a hierarchical manner.
MORE HEXAGONS
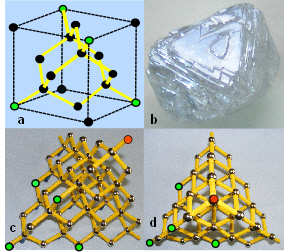 Hexagonal packing produces some natural structures that seem to be at the extremes of what is physically possible. Graphite consists of carbon atoms arranged in hexagonal configurations as layers of graphene.Keim Lots of these layers then stack on top of one another to produce a mineral that is a lubricant and very high conductor of electricity. Diamond, the hardest natural substance, is constructed from carbon atoms arranged in a 3-D hexagonal lattice, with complete hexagonal rings that form tetrahedral units, that crystallizes as an octahedron and uniquely has maximal cubic symmetry (all these polyhedra have cubic symmetry). It is unfortunate that cubes are taken as the standard representation of structure because clearly these other shapes are more fundamental (look at the pictures of the cube described earlier to see that the ‘edges’ are only approximations of straight lines).
Hexagonal packing produces some natural structures that seem to be at the extremes of what is physically possible. Graphite consists of carbon atoms arranged in hexagonal configurations as layers of graphene.Keim Lots of these layers then stack on top of one another to produce a mineral that is a lubricant and very high conductor of electricity. Diamond, the hardest natural substance, is constructed from carbon atoms arranged in a 3-D hexagonal lattice, with complete hexagonal rings that form tetrahedral units, that crystallizes as an octahedron and uniquely has maximal cubic symmetry (all these polyhedra have cubic symmetry). It is unfortunate that cubes are taken as the standard representation of structure because clearly these other shapes are more fundamental (look at the pictures of the cube described earlier to see that the ‘edges’ are only approximations of straight lines).
Sixty carbon atoms can unite as alternating hexagons and pentagons to form the ‘Buckyball’ fullerene based on the icosahedron. Single layers of graphene can also curve around to form cylindrical nanotubes that are amongst the toughest of materials.Terrones

