THE SIGNIFICANCE OF CLOSED KINEMATIC CHAINS TO BIOLOGICAL MOVEMENT AND DYNAMIC STABILITY
Journal of Bodywork and Movement Therapies
2017; 21:664-672 link
Stephen Levin
MD., FACS.
Susan Lowell de Solórzano
MA.
Graham Scarr
CBiol., FRSB., DO. request copy
ABSTRACT
Closed kinematic chains (CKCs) are widely used in mechanical engineering because they provide a simple and efficient mechanism with multiple applications, but they are much less appreciated in living tissues. Biomechanical research has been dominated by the use of lever models and their kinematic analysis, which has largely ignored the geometric organization of these ubiquitous and evolutionary-conserved systems, yet CKCs contribute substantially to our understanding of biological motion.
Closed-chain kinematics couple multiple parts into continuous mechanical loops that allow the structure itself to regulate complex movements, and are described in a wide variety of different organisms, including humans. In a biological context, CKCs are modular units nested within others at multiple size scales as part of an integrated movement system that extends throughout the organism and can act in synergy with the nervous system, where present. They provide an energy-efficient mechanism that enables multiple mechanical functions to be optimized during embryological development and increases evolutionary diversity.
KEYWORDS
Biomechanics; Biotensegrity; Closed-chain; Development; Evolution; Four-bar; Joint; Kinematics; Linkage; Morphology.
INTRODUCTION
Closed kinematic chains (CKCs) have been used in mechanical engineering since at least the beginning of the Industrial Revolution because they provide a simple and efficient mechanism with multiple applications (Phelan, 1962). They combine multiple parts into continuous mechanical loops, with each influencing the mechanical behaviour of all the others in the system, and enabling the controlled transfer and amplification (or attenuation) of force, speed and kinetic energy (fig. 1). However, while CKC linkages have been referred to as ‘complex lever systems’ (Alfaro et al., 2004), this description does not do them justice in a biological context because of the particular ways in which they relate to each other.
Modern anatomy has taken many centuries to accumulate a vast body of knowledge. It has classified structures according to the thinking of the day and sought to understand their functions using the latest technologies, but established conventions have allowed many important issues to be overlooked. The dissections of Vesalius (1514–1564) were important in overturning the dominant (but largely erroneous) anatomical wisdom that had prevailed since the time of Galen (c129–c200 CE), but his depictions of the musculo-skeletal duality have dominated our assessments of motion (Rifkin and Ackerman, 2006) and it is only relatively recently that the connective tissues have received the attention they deserve (Gracovetsky, 2008; Guimberteau and Armstrong, 2015; Schleip et al., 2012; Still, 1899).
Similarly, orthodox views of movement are essentially based on the mechanics of man-made machines described in the seventeenth century and a numerical system of kinematic analysis that greatly simplifies the anatomy (Brown and Loeb, 2000; Scarr and Harrison, 2016; Van Ingen Schenau, 1994), and although this approach has become the standard method of examining the forces and torques involved in joint motion (Rankin et al., 2016; Zajac et al., 2003), much less attention has been paid to the morphological geometry.
Biological CKCs are now examined from a more qualitative perspective that considers them as modular units nested within others at every size scale and part of an integrated movement system that extends throughout the organism (Levin, 2006; Turvey and Fonseca, 2014; Wilson and Kiely, 2016). Each part is structurally and functionally connected with all the others and contains a sequence of nested sub-systems that extends down to the cellular and molecular levels and is evolutionarily designed to respond to the specific loadings imposed (Simon, 1962; Clune et al., 2013; Kiely and Collins, 2016).
These linkage systems show how the position and orientation of each anatomical part results from the mechanical behaviour of a huge number of inter-linked tissues. They enable the structure itself to respond instantly to rapidly changing conditions and regulate complex movements in ways that are beyond the sole capability of the nervous system (Brown and Loeb, 2000; Kiely and Collins, 2016; Valero-Cuevas et al., 2007). The analysis of CKC geometries then reveals how multiple mechanical properties can be functionally compared between different parts of the body and other species, and optimized between different tissues during embryological development. It also provides a mechanism for increasing evolutionary diversity (Alfaro et al., 2004, 2005; Wainwright, et al., 2005).
CKC geometries have been described in the feeding mechanisms of crustaceans (Claverie et al., 2011; Summers, 2004), fish (Alfaro et al., 2004; Hulsey et al, 2005), amphibians (Kleinteich et al., 2008), reptiles (Kardong, 2003), the flight mechanics of insects (Miyan and Ewing, 1988; Walker et al., 2012) and birds (Biewener, 2011; Hedrick et al., 2012), and the limbs of mammals (Van Weeren et al, 1990) but are much less recognized in humans (Bradley et al., 1988; Huson, 1997).
Although ‘kinematic analysis’ and the lever model are widely used in biomechanics, the qualitative assessment of CKC geometries in living tissues has received little attention, with Vogel (2013, p. 401) declaring that “we mammals make no great use of multi-bar linkages”. It is thus the intention of this paper to highlight their significance as ubiquitous, mechanically-efficient and evolutionary-conserved structural arrangements with many advantages to human physiology, because kinematics is all about the geometry of motion.
THE 4-BAR KINEMATIC CHAIN
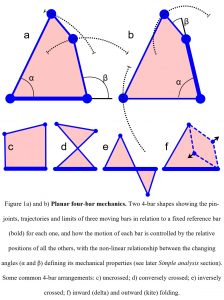
The simplest geometric arrangement that enables the structure itself to control motion is the planar 4-bar, where the length and position of each bar (linkage) determines the behaviour of all the others in the system, and the angular relationships between them define its mechanical properties (fig. 1). In comparison, 3-bar shapes (triangles) are crucially important because of their inherent stability, while those with five and more bars are uncontrollable on their own (although their importance in more complex systems is described later), which makes the planar 4-bar the best model to start describing this mechanism in biology (Muller, 1996).
The simplest geometric arrangement that enables the structure itself to control motion is the planar 4-bar, where the length and position of each bar (linkage) determines the behaviour of all the others in the system, and the angular relationships between them define its mechanical properties (fig. 1). In comparison, 3-bar shapes (triangles) are crucially important because of their inherent stability, while those with five and more bars are uncontrollable on their own (although their importance in more complex systems is described later), which makes the planar 4-bar the best model to start describing this mechanism in biology (Muller, 1996).
The coupling of multiple tissues
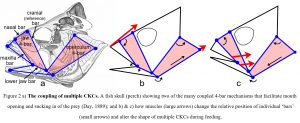The most thoroughly investigated 4-bar mechanisms in biology have been described in the feeding mechanisms of fish (Alfaro et al., 2004; Hulsey et al., 2005; Muller, 1996) (fig. 2) where the jaws, neurocranium, hyoid, suspensoria (cheeks) and opercula (gill covers) are part of multiple CKCs that are coupled together and mutually change shape; and permit the rapid expansion of the head and buccal cavity, mouth opening, sucking in and containment of the prey (Roos et al., 2009; Konow and Sanford, 2008). These mechanisms are also very efficient because they use a relatively small number of muscles to initiate complex movements in structures that are coupled together and operate in different planes.
Although there is considerable variation between species, such mechanisms enable those structures without direct muscular attachments to move with remarkable force and speed, and with a total prey capture period of less than fifty milliseconds in the large-mouth bass (Westneat and Olsen, 2015) and twenty-five milliseconds in the seahorse (Roos et al., 2009). Such quadratic feeding systems that couple upper jaw motion relative to the braincase have also been described in reptiles (Herrel et al., 1999; Montuelle and Williams, 2015) and birds (Bock, 1964; Gussekloo et al., 2001).
Amplification of force and speed
This ability of the 4-bar mechanism to amplify force and speed is well illustrated in the pantograph, where the output pen is able to move a greater distance and at a faster rate than the input stylus (fig. 3a). Its non-linear behaviour is intrinsically related to the geometry and is an emergent property that in a biological context enables the system to amplify muscular input and produce considerably greater amounts of force and speed, with the structure itself guiding motion. It is well demonstrated in the feeding mechanism of the mantis shrimp (Claverie et al., 2011; Summers, 2004) (fig. 3b).
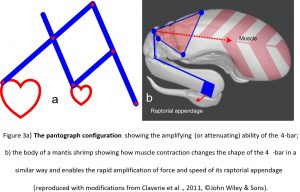Here, the large muscle situated within the thorax causes the chitinous 4-bar mechanism to change shape and propel the long raptorial appendage towards the target prey with a force of 1500 Newtons and within just three milliseconds; and with devastating effect (Patek and Caldwell, 2005). Such rapid jaw-closing movements are also found in ants (0.13 ms) (Patek et al., 2006), spiders (0.12 ms) (Wood et al., 2016) and termites (0.025 ms) (Seid et al., 2008) although the underlying mechanics have not been detailed as yet.
While many of these linkages in fish are constructed from stiff bone and cartilage (and chitin in the shrimp) it should be noted that the bars of some species are replaced by more flexible ligaments and/or variable length muscles (Hulsey et al., 2005; Roos et al., 2009), both of which enable other possibilities.
Tensional and compressional stiffness
Ligamentous links
In higher organisms, one of the best-known examples of these coupled linkages is in the knees of humans and other tetrapods (Haines, 1942), where the tensionally stiff cruciate ligaments contribute to regulating the motions of the femur and tibia in relation to each other (Bradley et al., 1988; Weissengruber et al., 2006); and the Jacob’s ladder toy nicely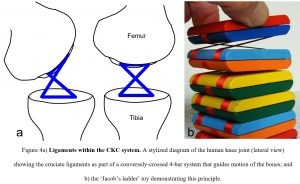 
demonstrates this principle (fig. 4). In this case, it is the tensional-stiffness of the ligaments that combines with the compressional-stiffness of the bones and contributes to guiding movement. Although ligaments have traditionally been considered as passive restrainers of motion it is clear that they can play more dynamic roles in joint mobility (Kim et al., 2002; Van der Wal, 2009).
Muscular links
Muscles are obviously prominent in biomechanical analysis because of their ability to initiate changes in position and movement through neural control, but while mono-articular muscles might be considered as variable-length bars within single-joint 3-bar systems, bi-articular muscles can form tensionally stiff bars within 4-bar CKCs that enable the motion of one joint to be directly coupled with that of another.
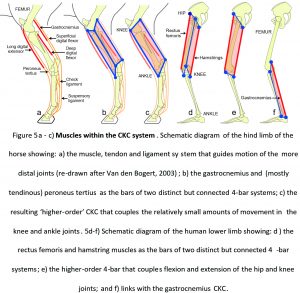
For example, the hind-legs of ungulates (hoofed animals) tend to have short muscle/long tendon combinations that control the relatively small movements of the knee, ankle and foot joints (Dimery et al., 1986; Biewener, 1998), with the bi-articular gastrocnemius muscle and (mostly tendinous) peroneus tertius contributing to two related but distinct 4-bar systems (Van Weeren et al., 1990) (figs. 5a, b). In detail, these are the peroneus tertius-femur-tibia-tarsals and gastrocnemius-femur-tibia-tarsals, respectively. Figure 5c then shows how the isometric contractions of these two muscles form stiff bars that balance each other within a ‘higher-order’ CKC system that guides, locks and stabilises movements of the knee and ankle.
In the lower limbs of humans, the bi-articular rectus femoris and hamstrings also act within their respective 4-bars (rectus femoris-pelvis-femur-tibia and hamstrings-pelvis-femur-tibia) to coordinate the much greater ranges of motion in the hip and knee joints, and contribute to a higher-order arrangement (figs. 5d, e). They also link with gastrocnemius and another 4-bar (gastrocnemius-femur-tibia-tarsals) that couples and guides knee and ankle movements (Van Ingen Schenau et al., 1987) (fig. 5f).
The ‘active’ tendon
The placement of muscles towards the more proximal part of the limb, and long tendons to control the distal part with each one operating within its own CKC network, is an evolutionary strategy that efficiently reduces limb inertia and the amount of effort needed to move (Cleland, 1867). Axially-stiff tendons can be routinely stretched up to six percent of their length and store elastic strain energy that can be released later, and because they can recoil much faster than muscles can shorten, enable the rapid elevation of the neurocranium during fish feeding (Van Wassenbergh et al., 2008) and a much greater
jumping ability than would otherwise be the case in horses (Biewener, 1998), wallabies (Biewener et al., 2004) and humans (Van Ingen Schenau, 1994).
Muscular force generators
This ability of bi-articular muscles to flex one joint whilst simultaneously extending another was recognized by both Galen (c130-c210) and Borelli (1608-1679) (Van Ingen Schenau, 1994) but did not really attract much attention until the nineteenth-century (Cleland, 1867), after which the mutual contraction of apparently antagonistic multi-joint muscles became known as ‘Lombard’s Paradox’ (Lombard, 1903; Kuo, 2001), but the full significance of this remained unclear.
In humans, the strongest muscles in the lower extremity are the mono-articular gluteus maximus, vastus lateralis and soleus (Lieber and Ward, 2011), with each one causing movement of the single joint that it crosses, but as muscles can only shorten by about 30 % of their resting length, they leave a potential shortfall in movement that must be filled by the action of others. Bi-articular muscles are able to fill this deficit because they can act effectively over the full range of both joints (fig. 5), or restrict the motion of one whilst enhancing that of the other, and an isometric contraction enables them to transfer energy from one joint to the other (Prilutsky and Zatsiorsky, 1994; Voronov, 2004).
While rapid muscle contractions generate a smaller amount of force than slow ones, the bi-articular (4-bar) configurations are able to compensate for this handicap by exhibiting a smaller length change, and reduced contractile velocity, than that of two mono-articular muscles for the same amount of joint motion (Lieber and Ward, 2011). They also include both groups of muscles in a more comprehensive scheme, as they transfer the combined power from one part of the body to another through a system of inter-linked CKCs, and have a profound effect on movement.
The transfer of power
For example, any attempt to jump from a standing position (hips and knees in extension) will result in rather poor performance, as the generation of power is largely limited to those muscles that plantar flex the ankle/foot, but jumping from a semi-crouched position can be quite different. In this case, contraction of the gluteus maximus and hamstrings in extending the hip can be coupled with the action of vastus lateralis and rectus femoris in extending the knee, and soleus and gastrocnemius in plantar flexing the ankle (figs. 5d-f), and enable the power generated by all these muscles to be effectively transferred to the ankle and foot (through changes in shape of the inter-linked CKCs) and cause a much greater amount of ‘lift off’ (Gregoire et al., 1984; Prilutsky and Zatsiorsky, 1994; Van Ingen Schenau et al., 1987).
As the positional status of each joint is dependent on the actions of both mono- and bi-articular muscles, the latter of which are inherently part of 4-bar systems that include multiple joints and force pathways, the effect of each muscle contraction can thus become distributed over a wide anatomical field (Stecco, 2004). The transference of power through the coupling of multiple CKCs may then be a contributing factor that enables such activities as rock climbing, where the entire body can move around and be supported from just the tips of the fingers; or the anecdotal ‘super-human’ ability to lift overly heavy objects, as the forces generated by multiple muscles are re-distributed in a task-specific way.
This inclusion of CKC mechanics into the normal physiology of movement thus questions the traditional notion of muscle ‘antagonism’ and reduces any enigma surrounding Lombard’s so-called paradox (Kuo, 2001; Lombard, 1903).
THE UBIQUITY OF CLOSED KINEMATIC CHAINS
Expanding the detail
Of course, all the examples given so far are gross simplifications of the anatomical reality but they do illustrate the basic principles of this mechanism. Two key properties that enable these systems to behave in the ways described are the axial stiffness of the bars and their closed-chain configuration, with each bar/CKC module directly influencing those adjacent to it and maintaining the dynamic stability that is inherent in movement. While bones, dense cartilage and chitin have a relatively high compressional-stiffness, so their more flexible ligamentous, tendinous and fascial counterparts (with tensional-stiffness and different mechanical properties) increase the versatility of this mechanism, and the addition of variable-length muscles as bars under neural control then dramatically expands its potential.
Multiple orientations
These CKCs have largely been considered as acting within a plane, which greatly simplifies their analysis (Muller, 1996), but they do not operate in isolation (Huson, 1997). The various bars that contribute to motion of the jaws, hyoid and operculum etc in fish are structurally and functionally coupled together but operate in different planes, with the power sources provided by both local and more distantly placed swimming muscles in the body wall (Camp et al., 2015; Westneat and Olsen, 2015) (fig. 2). Similarly, the varied origins and alignments of muscles that rotate the human hip joint will inevitably influence the spatial orientations of the ‘rectus femoris’, ‘hamstrings’ (fig. 5d) and other CKCs that couple the hip and knee together (‘sartorius’, ‘tensor fascia lata’ etc), and the same principle applies across every joint (Huson, 1997; Stecco, 2004).
Multi-link bars
It should also be noted that the linkage bars in certain species of fish consist of multiple bony and ligamentous elements (Roos et al., 2009; Hulsey et al., 2005), and that the muscle/tendon, rectus femoris/patella and ankle/foot bone combinations in horses and humans have all been considered as single bars for illustrative purposes (fig. 5). In reality, every anatomical structure is composed of smaller parts, with each one structurally and functionally connected with all the others and containing a sequence of nested sub-systems that extend down to the cellular and molecular levels (Simon, 1962); and the interactions between them are all contributing to the dynamic behaviour of the larger CKC system.
The global heterarchy
While anatomical classifications have traditionally used a hierarchical system of top-down ‘large important structures followed by smaller and less significant ones’, so this elucidation of CKC mechanics recognizes that all these tissues and the sub-structures that form them are in a reciprocal and mutual relationship, where the mechanical behaviour of each one potentially influences all the others at every size scale and warrants the term ‘heterarchy’ as a more inclusive descriptor (Turvey and Fonseca, 2014). Similarly, the ‘pin-joint’ connections between the bars are just a simplified short-hand that disguises the way in which these different axially-stiff tissues really interact with each other (figs. 2 – 5), and which explains why it is misleading to refer to these constructs as ‘complex lever systems’.
‘Pin-joints’ and levers
Pin-joints describe the points of rotation around which adjacent structures move and are widely used in movement analysis as a way of simplifying the resulting calculations (fig. 1), but living structures do not move around fixed fulcrums. Bones follow more complex helical pathways (Van den Bogert, 2008; Weissengruber et al., 2006) with all the tissues that connect them together contributing to this, and a moving fulcrum dramatically complicates their control.
To reiterate, the notion of fulcrums is part of lever theory and the standard biomechanical approach to examining the forces and torques involved in joint motion, both of which are based on the working of man-made machines; but as levers inherently generate bending moments and potentially damaging stress concentrations that must be contained within the engineered design (Salvadori, 2002, p. 84), so it is likely that these stresses would cause material fatigue if they appeared in developing tissues, and that would really be the end of them (Levin, 1995).
Lever theory has undoubtedly provided valuable information in the development of artificial joints, limbs and robotics but essentially dictates that synovial joint surfaces must be compressed; and it has been definitively shown that normal joint surfaces in the human knee do not behave like this (Hakkak et al., 2015; Levin and Madden, 2005; Terayama et al., 1980), which thus questions the reliability of lever theory to describing the actual biology.
The current use of the term ‘pin-joints’ thus recognizes that both the bars and the connections between them are multiple structures acting within their own closed-chain modular systems at different size scales, and because there is no true fulcrum or bending-moment around which a lever can act, any formulaic prediction about joint function will always be an approximation (Brown and Loeb, 2000; Humphrey, 2003); a point that is frequently overlooked.
Biotensegrity
This integration of multiple parts into a more comprehensive movement system is thus fully compatible with the concept of biotensegrity: a structural design principle that recognizes that stability and ease of movement are not due to the strength of individual components but because of the way the entire system is configured to distribute mechanical forces (Levin, 1995, 2006; Scarr, 2014; Wilson and Kiely, 2016) (fig. 6).
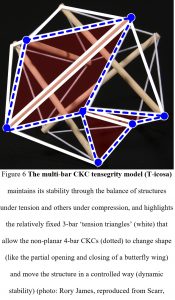Biotensegrity considers that a living organism is really a complex balance of force vectors, and that it is the efficient separation of the forces of tension and compression into different structural modules (‘bars’) that enables them all to change shape with the minimum of effort and automatically return to the same position of stable equilibrium. The compressed and tensioned bars within any particular CKC module are then not acting on their own but within a much larger inter-linked structural entity, with the configuration enabling each one to mechanically influence the behaviour of all the others in the system yet remain completely stable (dynamic stability) throughout such changes (Scarr and Harrison, 2017).
Biotensegrity offers distinct advantages in cyclic systems, where each part must move in a coordinated way that rapidly adapts to the ever-changing environment but whose control is beyond the sole capability of neural processing networks (Brown and Loeb, 2000; Kiely and Collins, 2016).
The control of motion
While the motor cortex and central pattern generators regulate cyclic and purposeful movements, complex reflex patterns in the brainstem and spinal cord exchange information between different parts of the movement system, and they all depend on a vast amount of sensory input. Reflex systems assimilate this and initiate muscle contractions in ways that supplement supra-spinal control, but their ability to respond to unexpected changes within the system is incomplete as even the fastest mono-synaptic reflex experiences a time-delay (Brown and Loeb, 2000).
A regulatory system that is embedded within the structure itself thus has a distinct evolutionary advantage (Kiely and Collins, 2016; Levin, 2006; Turvey and Fonseca, 2014) as the interactions between multiple force vectors and CKC modules guide changes in the position of each part and the nervous system (where present) acts at a higher level of control.
The information processing network
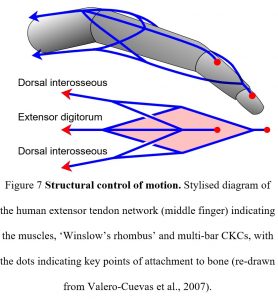For example, Valero-Cuevas et al (2007) noted that there are an insufficient number of muscles to determine all the different finger joint positions on their own and that the extensor tendon network (CKCs) operates synergistically with the nervous system in regulating their motion (fig. 7). Here, the tensional forces generated by each muscle contraction are transferred to the three-dimensional connective tissue network through long tendons, but they do not simply move the bones. It is the relative differences in tension that alter the balance of forces within the network and switches the system between different functional states, thus changing the position of the bones in relation to each other and the ‘shape’ of the finger. It is the structure itself that is processing the information (force and direction) and performing its own logic computations that were previously attributed to the central nervous system.
Such a three-dimensional, polyhedral, multi-bar network of fibres (CKCs) has also been demonstrated within the extra-cellular matrix/fascia, where the tensioned fibres (‘bars’) coalesce and separate into different geometric arrangements, according to the forces acting on them during movement, and influence all the structures that they connect to (Guimberteau and Armstrong, 2015). Dynamic information processing has also been described in the cellular cytoskeleton, a complex structural network that integrates chemical signals with mechanical forces exerted by the extra-cellular matrix and surrounding cells, and switches the cell between different functional states (Ingber, 2003; Ingber et al., 2014).
Multi-bar organization
Modular closed-chain organization is thus ubiquitous throughout the body and a major contributor to the dynamics of motion, and it is non-trivial. This elucidation focuses on planar 4-bar geometry because it explains so many of the basic principles, but these also extend to multi-bar configurations that are oriented in many different planes and increase the number of degrees-of-freedom; (Muller, 1996; Guimberteau and Armstrong, 2015; Kardong, 2003; Rimoli, 2016).
Although five and more-bar modules probably constitute the majority of biological CKCs, they are mechanically indeterminate on their own, but their integration within a more comprehensive nested system greatly increases the multi-directional motion and control possibilities. While the foregoing has essentially been a qualitative assessment of CKC organization there are also other ways to examine its characteristics.
The emergence of shape
Biological CKCs can sometimes appear rather random and arbitrary (particularly at the microscopic scale) but can be compared with the bubbles in a foam, where each one simply moves in response to the stresses imposed by its neighbours (and the system as a whole), and the same basic principle applies at every heterarchical level (Kapandji, 2012; Levin, 2006). While mechanical engineering has made great progress in analysing closed-chain lever systems (Phelan, 1962), it uses methods that are not ideally suited to living tissues, which prompted Muller (1996) to introduce a biologically-relevant classification that enables their mechanical behaviour to be compared between different parts of the organism and across a wide range of different species; and which highlights useful information about embryological and evolutionary processes.
Simple analysis
Figure 1 showed how the motion of each bar is controlled by the relative positions of all the others, with the ratio between the input (α) and output (β) angles on either side of each reference bar defining the mechanical properties, kinematic transmission – KT. The value of Muller’s (1996) novel system is that it condenses the virtually infinite number of different 4-bar shapes to a level that can be meaningfully examined and graphically compares the changing angular relationships between the bars during motion. It uses just fourteen different shapes and two parameters (bar length and arrangement) to distinguish between them.
Figure 8 shows three of Muller’s (1996) shapes with the curves displaying the changing KT (ratios) during motion and the different contours showing the effect of altering the relative lengths of the bars. Although incremental changes in relative bar length would eventually cause all the shapes and KT curves to merge into a multi-dimensional continuum, the pattern of each curve is distinctive enough to allow the changing mechanical properties of any 4-bar shape to be graphically compared and new insights gained.
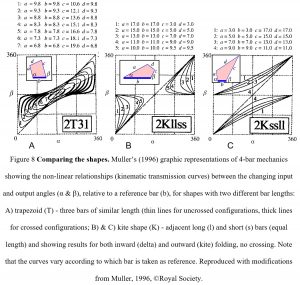Muller’s (1996) classification looks at the complexity inherent in biological systems by simply comparing the effect of changes in the relative lengths of the component bars and the overall geometry, and this graphic representation shows that 4-bar mechanics differ substantially from those of the traditional lever model in two important respects.
First, their changing morphology (shape) maps non-linearly to KT, an emergent property where changes in shape lead to disproportionate changes in response and which enable the amplification (or attenuation) of force, speed and kinetic energy.
Secondly, the shape of the 4-bar maps redundantly to KT, which means that different combinations of bar lengths can produce the same mechanical property (KT); and this ‘many-to-one’ (MTO) relationship then has evolutionary implications as it permits a partial decoupling between morphological diversity and function (Alfaro et al., 2004, 2005; Wainwright et al., 2005).
Many-to-one mapping
For example, a particular CKC shape will have multiple functions such as lower jaw depression, maxillary rotation and nasal elevation in fish (fig. 2) and it is the relative lengths of the bars that determine its overall shape and mechanical properties. Alfaro et al. (2004, 2005) and Wainwright et al. (2005) then used a 3-D graphic representation to compare the effect of changes in the relative lengths of the bars and revealed the full range of different 4-bar shapes with the same mechanical property (KT ratio), and a group of fish species with different jaw morphologies that all functioned in a similar way.
Such redundancy is an emergent property of MTO mapping and shows that the length of the bars can change (through growth and other developmental processes) and alter the CKC shape (morphology), while still keeping the same mechanical functions overall, and that there are many ways of achieving the same outcome. As a developing organism must remain stable at each instant of its existence, CKC organization allows each part to change in length and shape (morphology) while at the same time enabling multiple mechanical properties to be optimized across the global network. It also provides a mechanism for increasing evolutionary diversity (Alfaro et al., 2004, 2005; Wainwright et al., 2005).
It is all about efficiency
The spontaneous appearance of particular geometric shapes in self-organizing systems is due to the most energy-efficient arrangements of their component parts (bars), and the resulting mechanical behaviours (e.g. non-linearity) are characteristic features that emerge out of this (fig. 8) and are intrinsic to living systems. The ability of multiple structures to perform the same function (redundancy) is an evolutionary strategy that enables the system to efficiently distribute forces over a variety of different pathways and compensate for any deficits that arise within the system; and as a degenerate system, it would also enable the co-operation of fundamentally different [modular] components to produce consistently reliable outputs under diversely fluctuating conditions (Wilson and Kiely, 2016).
Whenever nature uses the same strategy in a variety of different situations there is probably an underlying energetic advantage, and embryological development and evolution consistently favours those patterns and shapes that are the most efficient in terms of stability, materials and mass. While the flow of energy within a living organism will always tend towards a minimal and dynamically stable state, the emergence of modularity within a global heterarchy becomes a crucial organizing principle in what would otherwise be a completely chaotic system (Clune et al., 2013; Simon, 1962), and the appearance of non-linearity, redundancy and degeneracy within a global CKC system contribute to that process.
CONCLUSION
Examination of closed-kinematic chains across a wide range of species reveals a ubiquitous and evolutionarily-conserved modular arrangement that extends throughout the organism at every size scale. Each part is structurally and functionally connected with all the others in a mechanical system that responds instantly to rapidly changing conditions and can act in synergy with the nervous system (where present), thus enabling power to be transferred from one part of the body to another in a task-specific way.
CKCs show how the position and orientation of each anatomical part results from the mechanical behaviour of a huge number of inter-linked structures, with each one adjusting itself in response to the loadings imposed and adapting to changing functional demands, and all within a global biotensegrity configuration. The characteristics of modularity, non-linearity, redundancy and degeneracy then typify the efficient self-organizing ability of living systems, where definable shapes and functions emerge from complex interactions between multiple parts and dynamically evolve towards a more energy-efficient state.
A view of human anatomy as a global network of interconnected CKCs means that the structures associated with motion can no longer be considered as distinct entities but mechanically coupled linkages that reciprocally influence each other within a much broader scheme. So, far from “we mammals make no great use of multi-bar linkages” (Vogel, 2013 p. 401), closed kinematic chains now define a ubiquitous, multi-tasking structural system that contributes to a more comprehensive assessment of motion.
The authors are independent researchers and received no funding from agencies in the public, commercial, or not-for-profit sectors. There are no Conflicts of Interest to declare.
REFERENCES
Alfaro, M.E., Bolnick, D.I., Wainwright, P.C., 2004. Evolutionary dynamics of complex biomechanical systems: an example using the four-bar mechanism. Evolution 58, 495-503.
Alfaro, M.E., Bolnick, D.I., Wainwright, P.C., 2005. Evolutionary consequences of many-to-one mapping of jaw morphology to mechanics in labrid fishes. Am. Natural. 165, E140-E154.
Biewener, A.A., 1998. Muscle-tendon stresses and elastic energy storage during locomotion in the horse. Compar. Biochem. Physiol. B. 120, 73-87.
Biewener, A.A., McGowan, C., Card, G.M., Baudinette, R.V., 2004. Dynamics of leg muscle function in tammar wallabies (M. Eugenii) during level versus incline hopping. J. Exp. Biol 207, 211-223.
Biewener, A.A., 2011. Muscle function in avian flight: achieving power and control. Phil. Trans. R. Soc. B. 366, 1496-1506.
Bock, W.J., 1964. Kinetics of the avian skull. J Morphol. 114, 1-42.
Bradley, J., FitzPatrick, D., Daniel, D., Shercliff, T., O’Connor, J., 1988. Orientation of the cruciate ligament in the sagittal plane: a method of predicting its length-change with flexion. Brit. J. Bone Joint Surg. 70, 94-99.
Brown, I.E., Loeb, G.E., 2000. A reductionist approach to creating and using neuromuscular models. In: Winsters, J.M., Crago, P.El (Eds.), Biomechanics and Neural Control of Posture and Movement. Springer-Verlag, New York, pp. 148-163.
Camp, A.L., Roberts, T.J., Brainerd, E.L., 2015. Swimming muscles power suction feeding in largemouth bass. PNAS 112, 8690-8695.
Claverie, T., Chan, E., Patek, S.N., 2010. Modularity and scaling in fast movements: power amplification in mantis shrimp. Evolution. 65, 443-461.
Cleland, J., 1867. On the actions of muscles passing over more than one joint. J. Anat. Physiol. 1, 85-93.
Clune, J., Mouret, J.B., Lipson, H., 2013. The evolutionary origins of modularity. Proc. R. Soc. B. 280, 20122863. http://dx.doi.org/10.1098/rspb.2012.2863.
Day, F., 1889. Head of perch. Wikipedia, public domain, https://commons.wikimedia.org/wiki/File:FishKeyDay_(cropped).jpg
Dimery, N.J., Alexander, R.M., Ker, R.F., 1986. Elastic extension of leg tendons in the locomotion of horses (Equus caballus). J. Zool. Lond. A. 210, 415-425.
Gracovetsky, S., 2008. Is the lumbodorsal fascia necessary? J. Bodyw. Mov. Thera. 12, 194-197.
Gregoire, L., Veeger, H.E., Huijing, P.A., van Ingen Schenau, G.J., 1984. Role of mono-and biarticular muscles in explosive movements. Int. J. Sports Med. 5, 301-305.
Guimberteau, J.C., Armstrong, C., 2015. Architecture of human living fascia: the extracellular matrix and cells revealed through endoscopy. Handspring, Edinburgh.
Gussekloo, S.W.S., Vosselman, M.G., Bout, R.G., 2001. Three-dimensional kinematics of skeletal elements in avian prokinetic and rhynchokinetic skulls determined by roentgen stereophotogrammetry. J. Exp. Biol. 204, 1735-1744.
Haines, R.W., 1942. The tetrapod knee joint. J. Anat. 76, 270–301.
Hakkak, F., Jabalameli, M., Rostami, M., Parnianpour, M., 2015. The tibiofemoral joint gaps – an arthroscopic study. SDRP J. Biomed. Eng. 1, 1-6.
Hedrick, T.L., Tobalske, B.W., Ros, I.G., Warrick, D.R., Biewener, A.A., 2012. Morphological and kinematic basis of the hummingbird flight stroke: scaling of flight muscle transmission ratio. Proc. R. Soc. B. 279, 1986-92.
Herrel, A., De Vree, F., Delheusy, V., Gans, C., 1999. Cranial kinesis in gekkonid lizards. J. Exp. Biol. 202, 3687-3698.
Hulsey, C.D., Fraser, G.J., Streelman, J.T., 2005. Evolution and development of complex biomechanical systems: 300 million years of fish jaws. Zebrafish 2, 243-257.
Humphrey, J.D., 2003. Continuum biomechanics of soft biological tissues. Proc. R. Soc. Lond. A. 459, 3-46.
Huson, A., 1997. Kinematic models and the human pelvis., in: Vleeming, A., (Ed.), Movement, stability and low back pain: the essential role of the pelvis. Churchill Livingstone, New York, pp. 123-131.
Ingber, D.E., 2003. Tensegrity II. How structural networks influence cellular information processing networks. J. Cell Sci. 116, 1397-1408.
Ingber, D.E., Wang, N., Stamenović, D., 2014. Tensegrity, cellular biophysics and the mechanics of living systems. Rep. Prog. Phys. 77, 046603.
Kapandji, A.I., 2012. Le système conjonctif, grand unificateur de l’organisme. Annales de chirurgie plastique esthètique 57, 507-514.
Kardong, K.V., 2003. Biomechanics and evolutionary space: a case study., Chapter 5 in: Bels, V.L., Gasc, J.P., Casinos, A., (Eds.), Vertebrate biomechanics and evolution. BIOS Scientific Publishers Ltd, Oxford, pp. 73-86.
Kiely, J., Collins, D.J., 2016. Uniqueness of human running coordination: the integration of modern and ancient evolutionary innovations. Front. Psychol. 7, 1-8.
Kim, P., Isogai, S., Murakami, G., Wada, T., Aok,i M., Yamashita, T., Ishii, Seiichi., 2002. The lateral collateral ligament complex and related muscles act as a dynamic stabiliser as well as a static supporting structure at the elbow joint: an anatomical an experimental study. Okajimas Folia Anat Jpn. 79, 55-62.
Kleinteich, T., Haas, A., Summers, A.P., 2008. Caecilian jaw-closing mechanics: integrating two muscle systems. J. R. Soc. Inter. 5, 1491-1504.
Konow, N., Sanford, C.P.J., 2008. Biomechanics of a convergently derived prey-processing mechanism in fishes: evidence from comparative tongue bite apparatus morphology and raking kinematics. J. Exp. Biol. 211, 3378-3391.
Kuo, A.D., 2001. The action of two-joint muscles: the legacy of W.P. Lombard., Chapter 10 in: Latash, M., Zatsiorsky, V. (Eds.), Classics in movement science., Champagne., IL: Human Kinetics, pp. 289-316.
Levin, S.M., 1995. The importance of soft tissues for structural support of the body., in: Dorman, T.,(Ed.), Spine: state of the art reviews 9, Hanley and Belfus, Philadelphia, pp. 357-363.
Levin, S.M., Madden, M.A., 2005. In vivo observation of articular surface contact in knee joints. (Available online at: www.biotensegrity.com [Accessed 10th November, 2016].)
Levin, S.M., 2006. Tensegrity: the new biomechanics., in: Hutson, M., and Ellis, RE. (Eds.) Textbook of musculoskeletal medicine., Oxford University Press, Oxford, pp. 69-80.
Lieber, R.L., Ward, S.R., 2011. Skeletal muscle design to meet functional demands. Phil. Trans. R. Soc. B. 366, 1466-1476.
Lombard, W.P., 1903. The tendon action and leverage of two-joint muscles of the hind leg of the frog, with special reference of the spring movement., in: Wahr, G., (Ed.), Contributions to Medical Research, Ann Arbor Sci. Pub., MI, pp. 280-301.
Miyan, J.A., Ewing, A.W., 1988. Further observations on dipteran flight: details of the mechanism. J. Exp. Biol. 136, 229-241.
Montuelle, S.J., Williams, S.H., 2015. In vivo measurement of mesokinesis in Gekko gecko: the role of cranial kinesis during gape display, feeding and biting. PLOS ONE 10, e0134710
Muller, M., 1996. A novel classification of planar four-bar linkages and its application to the mechanical analysis of animal systems. Phil. Trans. R. Soc. Lond. B. 351, 689-720.
Patek, S.N., Caldwell. R,L., 2005. Extreme impact and cavitation forces of a biological hammer: strike forces of the peacock mantis shrimp Odontodactylus scyllarus. J. Exp. Biol. 208, 3655-3664.
Patek, S.N., Baio, J.E., Fisher, B.L., Suarez, A.V., 2006. Multifunctionality and mechanical origins: ballistic jaw propulsion in trap-jaw ants. PNAS 103, 12787-12792.
Phelan, R.M., 1962. Fundamentals of mechanical design. 2nd ed., McGraw-Hill Book Co, London.
Prilutsky, B.I., Zatsiorsky, V.M., 1994. Tendon action of two-joint muscles: transfer of mechanical energy between joints during jumping, landing and running. J. Biomech. 27, 25-34.
Rankin, J.W., Rubenson, J., Hutchinson, J.R., 2016. Inferring muscle functional roles of the ostrich pelvic limb during walking and running using computer optimization. J. R. Soc. Interface 13: 20160035.
Rifkin, B.A., Ackerman, M.J., 2006. Human anatomy: a visual history from the Renaissance to the digital age. Abrams, New York.
Rimoli, J.J., 2016. On the impact tolerance of tensegrity-based planetary landers. 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 4th-8th Jan., San Diego, CA. DOI: 10.2514/6.2016-1511.
Roos, G., Leysen, H., Van Wassenbergh, S., Herrel, A., Jacobs, P., Dierick, M., Aerts, P., Adriaens, D., 2009. Linking morphology and motion: a test of a four-bar mechanism in seahorses. Phyiol. Biochem. Zool. 82, 7-19.
Salvadori, M., 2002. Why buildings stand up: the strength of architecture. W.W. Norton & Co, Inc., New York.
Scarr, G. 2014. Biotensegrity: the structural basis of life. Handspring, Edinburgh.
Scarr, G., Harrison, H., 2016. Resolving the problems and controversies surrounding temporo-mandibular mechanics. J. Appl. Biomed. 14, 177-185.
Scarr, G., Harrison, H., 2017. Examining the temporo-mandibular joint from a biotensegrity perspective: a change in thinking. J. Appl. Biomed. 15, 55-62.
Schleip, R., Findley, T.W., Chaitow, L., Huijing, P.A., (Eds.), 2012. Fascia: the tensional network of the body, Elsevier, Edinburgh.
Simon, H.A., 1962. The architecture of complexity. Proc. Am. Phil. Soc. 106, 467-482.
Seid, M.A., Scheffrahn, R.H., Niven, J.E., 2008. The rapid mandible strike of a termite soldier. Curr. Biol. 18, R1049-R1050.
Stecco, L., 2004. Fascial manipulation for musculoskeletal pain. Piccin Nuova Libraria, Padova.
Still, A. T., 1899. Philosophy of Osteopathy. (self-published) Kirksville, MO.
Summers, A., 2004. Knockout punch: a boxer who could jab like a mantis shrimp could win every match with a single blow. Nat. Hist. Mag. 114, 22-23.
Terayama, K., Takei, T., Nakada, K., 1980. Joint space of the human knee and hip joint under a static load. Engineering in Medicne 9, 67-74.
Turvey, M.T., Fonseca, S., 2014. The medium of haptic perception: a tensegrity hypothesis. J. Mot. Behav. 46, 143-187.
Valero-Cuevas, F.J., Yi, J.W., Brown, D., McNamara, R.V., Chandana, P., Lipson, H., 2007. The tendon network of the fingers performs anatomical computation at a macroscopic scale. IEEE Trans. Biomed. Eng. 54, 1161-1166.
Van den Bogert, A.J., 2003. Exotendons for assistance of human locomotion. BioMed. Eng. OnLine 2, 17.
Van den Bogert, A.J., 2008. Helical axes of skeletal knee joint motion during running. J. Biomech. 41, 1632-1638.
Van der Wal, J., 2009. The architecture of the connective tissue in the musculoskeletal system: an often overlooked functional parameter as to proprioception in the locomotor apparatus. Int. J. Ther. Massage Bodyw. 2, 9-23.
Van Ingen Schenau, G.J., 1994. Proposed actions of bi-articular muscles and the design of hindlimbs of bi-and quadrupeds. Hum. Mov. Sci. 13, 665-681.
Van Ingen Schenau, G.J., Bobbert, M.F., Rozendal, R.H., 1987. The unique action of bi-articular muscles in complex movements. J. Anat. 155, 1-5.
Van Wassenbergh, S., Strother, J.A., Flammang, B.E., Ferry-Graham, B.E., Aerts, P., 2008. Extremely fast prey capture in pipefish is powered by elastic recoil. J. R. Soc. Inter. 5, 285-296.
Van Weeren, P.R., Van den Bogert, A.J., Barneveld, A., Hartman, W., Kersjes, A.W., 1990. The role of the reciprocal apparatus in the hind limb of the horse investigated by a modified CODA-3 opto-electronic kinematic analysis system. Equine Vet. J. Suppl. 9, 95-100.
Vogel, S., 2013. Comparative biomechanics: life’s physical world., 2nd ed., Princeton University Press, Princeton.
Voronov, A.V., 2004. The roles of monoarticular and biarticular muscles of the lower limbs in terrestrial locomotion. Hum. Physiol. 30, 476-484.
Wainwright, P.C., Alfaro, M.E., Bolnick, D.I., Hulsey, C.D., 2005. Many-to-one mapping of form to function: a general principle in organismal design? Integr. Comp. Biol. 45, 256-262.
Walker, S.M., Thomas, A.L.R., Taylor, G.K., 2012. Operation of the alula as an indicator of gear change in hoverflies. J. R. Soc. Inter. 9, 1194-1207.
Weissengruber, G.E., Fuss, F.K., Egger, G., Stanek, G., Hittmair, K.M., Forstenpointner, G., 2006. The elephant knee joint: morphological and biomechanical considerations. J. Anat. 208, 59-72.
Westneat, M.W., Olsen, A.M., 2015. How fish power suction feeding. PNAS 112, 8525-8526.
Wilson, J., Kiely, J., 2016. The multi-functional foot in athletic movement: extraordinary feats by our extraordinary feet. Human Mov.17, 15-20.
Wood, H.M., Parkinson, D.Y., Griswold, C.E., Gillespie, R.G., Elias, D.O., 2016. Repeated evolution of power-amplified predatory strikes in trap-jaw spiders. Curr. Biol. 26, 1057-1068.
Zajac, F.E., Neptune, R.R., Kautz, S.A., 2003. Biomechanics and muscle coordination of human walking; Part II: lessons from dynamical simulations and clinical implications. Gait Posture 17, 1-17.