Myofascial Helices
FASCIAL HIERARCHIES AND THE RELEVANCE OF CROSSED-HELICAL
ARRANGEMENTS OF COLLAGEN TO CHANGES IN THE SHAPE OF MUSCLES
Journal of Bodywork and Movement Therapies
2016; 20:377-387 link
Graham Scarr request copy
KEYWORDS
Collagen; Crossed-helix; Crossed-ply; Epimysium; Fascia; Helix; Muscle; Myofascia; Pennation; Perimysium.
ABSTRACT
Muscles are composite structures consisting of contractile myofibres surrounded by complex hierarchies of collagen-reinforced fascial sheaths. They are essentially flexible cylinders that change in shape, with the particular alignment of collagen fibres within their myofascial walls reflecting the most efficient distribution of mechanical stresses and coordinating these changes. However, while the functional significance of this crossed-helical fibre arrangement is well established in other species and in different parts of the body, relatively little attention has been given to this within the fascia of humans; and the relevance of this geometric configuration to muscles and surrounding fascial tissues is described.
INTRODUCTION
The Fascia
The importance of the fascia to normal function has been recognized by ‘hands-on’ practitioners for more than a century (Still 1899; Findley and Shalwala 2013) but it is only recently that it has emerged as a significant contributor to mainstream orthopaedic knowledge (Schleip et al 2012). Once dismissed as a packing tissue of little consequence, the fascia is now recognized as a continuous interconnected network that permeates and envelops almost every part of the body and is now taking its rightful place at the ‘top table’ of anatomical and physiological research.
The term ‘fascia’ refers to dense planar tissue sheets such as the ‘deep’ or ‘investing’ fascia (fascia profunda), septa, aponeuroses, joint and organ capsules, the epimysium that surrounds muscles; and the softer ‘superficial’ fascia beneath the skin, the intra-muscular endomysium that surrounds individual muscle fibres; and perimysium that surrounds bundles of these fibres. It also includes the dura mater, periosteum, neurovascular sheaths and abdominal mesentery etc, and is continuous with ‘non-fascial’ densifications in the form of ligaments, tendons (Benjamin 2009; Schleip et al 2012), periosteum and bone (Aaron 2012).
The internal structure of these fascial sheets consists of an extra-cellular matrix (ECM) containing highly hydrated proteoglycan complexes (‘ground substance’) and a variety of cells and interlinked fibres (Gillies and Lieber 2011), and is continuous with the ECM that surrounds virtually every cell in the body. A fibrillar collagen and elastin network also encloses proteoglycan ‘microvacuoles’, which surround and blend with tendons, aponeuroses, skin, nerves and blood vessels etc so that at the microscopic level there is no distinct boundary between where one ends and another begins (Guimberteau 2005; 2012).
Unfortunately, it is this anatomical continuity and the pervasiveness of fascial tissues at every size scale that has confounded anatomists over the centuries and maintained this connective tissue matrix as the “Cinderella of orthopedic science” (Schleip et al 2012 p xv); but a new and all encompassing classification system based on density and fibre alignment is now able to relate them all together in a useful way (Schleip et al 2012 p xvii). The myofascia is then just a fibrous specialization that is intimately connected with muscle, and the crossed-helical orientation of collagen fibres within it and the surrounding fascia play important functional roles that deserve wider recognition.
THE FASCIA
Myofascia
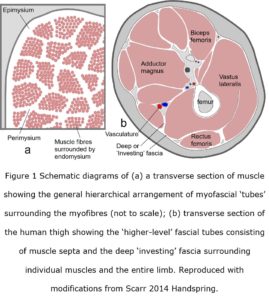 The myofascia is traditionally classified into three different regions (Turrina et al 2013), which together form a hierarchical network of fibrous tubes or sheaths enclosing smaller tubes within them, and is continuous with ‘higher-level’ fascial tubes (compartments) that surround groups of muscles, the limbs and entire body (figure 1). Although some authors consider that the myofascia should no longer be considered as a collection of ‘tubes’ or ‘sheaths’, as it is really a “three-dimensional matrix that is continuous throughout the entire organ” (Purslow and Delage 2012 p 5) and “tremendously complex compared with other connective tissues” (Gillies and Lieber 2011 p 318), a comparison with crossed-helical ‘tubes’ in other parts of the body and in different species suggests that an appreciation of this pattern is important to furthering our understanding of muscle mechanics (Clarke and Cowey 1958; Kier and Smith 1985).
The myofascia is traditionally classified into three different regions (Turrina et al 2013), which together form a hierarchical network of fibrous tubes or sheaths enclosing smaller tubes within them, and is continuous with ‘higher-level’ fascial tubes (compartments) that surround groups of muscles, the limbs and entire body (figure 1). Although some authors consider that the myofascia should no longer be considered as a collection of ‘tubes’ or ‘sheaths’, as it is really a “three-dimensional matrix that is continuous throughout the entire organ” (Purslow and Delage 2012 p 5) and “tremendously complex compared with other connective tissues” (Gillies and Lieber 2011 p 318), a comparison with crossed-helical ‘tubes’ in other parts of the body and in different species suggests that an appreciation of this pattern is important to furthering our understanding of muscle mechanics (Clarke and Cowey 1958; Kier and Smith 1985).
Endomysium
The endomysium is a delicate tissue that surrounds individual muscle fibres (myofibres) and links them all within a continuous honeycomb arrangement that extends laterally across each fascicle and over the entire length of the muscle (Purslow and Trotter 1994; Nishimura et al 1996) (figure 2). It consists of a basement membrane that covers the sarcolemma (plasma membrane) and contains mostly type IV collagen, and a thicker felt-like reticular layer of collagen fibres of predominantly types III, V and VI with only small amounts of type I.
This network forms an intimate connection with the myofibril and enables the transfer of contractile force (Huijing 2012a; Turrina et al 2013), and because the tubular wall of this endomysial sheath is shared between adjacent myofibres, the tensional force generated by contraction can be efficiently transmitted to adjacent tubes through what is described as trans-laminar shear (Purslow and Trotter 1994; Purslow 2002). Even the terminations of serially arranged myofibres, which are often staggered by about a quarter of their length with respect to adjacent myofibres, must transmit their force in the same way (Gaunt and Gans 1992; Sharafi and Blemker 2011) as this endomysial network is the only structure that continuously links them all together within a fascicle (Purslow 2010; Turrina et al 2013). Such lateral load sharing maintains a uniform strain throughout the tissue and is transversely isotropic (Passerieux 2006; Sharafi and Blemker 2010; Chaudhry et al 2012) as well as enabling muscles to grow and repair damaged sarcomeres without loss of force transfer through the contractile column (Purslow 2010).
While the endomysium ultimately transmits the tensional force generated by myofibre contraction to the tendons (Turrina et al 2013), it is also “very compliant to tensile forces acting within the plane of the network and… can easily deform to follow the length and diameter changes of muscle fibers in contracting and relaxing muscles” (Purslow and Delage 2012 p 7), making this highly nonlinear elastic material a key component in muscle flexibility (Meyer and Lieber 2011).
Perimysium
The perimysium, however, is a much more complex myofascial tissue and one with key functions that remain unresolved, with collagen types I, III, IV, V, VI, XII and XIV predominating and large variations in thickness, fibre size, orientation and attachment adding to this complexity (Passerieux et al 2006; Gillies and Lieber 2011). The perimysium is continuous with the outer epimysium and tendons at either end of the muscle, and has direct attachments to both myofibres and their endomysial sheaths (Purslow 2010; Gillies and Lieber 2011).
Although both endomysial and perimysial tissues are regarded as qualitatively similar across different species such as bovines, porcines, murines and humans etc (Rowe 1981), variations do occur between them and in different muscles within the body, and can complicate detailed comparisons. Several levels of organization have been described, including the larger fascicles that bundle groups of myofibres (10 – 100) and their endomysium together (figure 1a), to the smaller fascicles that arise from them and subdivide into successively smaller bundles (Purslow 2010; Chaudhry et al 2012). Terms such as ‘primary’ and ‘secondary’ fascicles, however, will not be mentioned further as they relate to relative size and are used inconsistently in the literature. In contrast to the endomysium, micro-mechanical modelling shows that the behaviour of perimysial fascicles is transversely anisotropic to changes in shape (Sharafi and Blemker 2010).
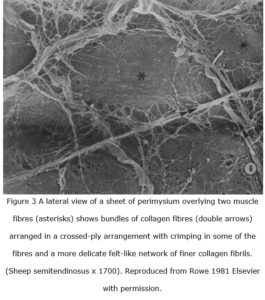
The ‘walls’ of these perimysial fascicles consist primarily of two or more layers containing large flattened cables or bundles of wavy (crimped) collagen type I fibres, which are oriented parallel to the myofibres in the region of the myotendinous junction but generally curve around the fascicle wall with an oblique angle (Passerieux et al 2007). The cables are generally aligned at an angle of ~55o relative to the myofibre axis in resting muscle, and each alternating layer is oriented differently so that the tubular wall appears as a crossed-ply network with the cables spaced at regular intervals and parallel to each other (Gillies and Lieber 2011; Purslow 2010). In addition, thin strips of perimysial tissue extend laterally from the smaller fascicle walls and pass between the myofibres (Passerieux et al 2007) with the collagen fibres aligned in both felted and criss-cross arrangements (Rowe 1981) (figure 3).
 The points of intersection between these oriented collagen fibres then give rise to branching plexuses that ultimately connect to the surface of adjacent myofibres (and their endomysium) through perimysial junctional plates (PJP’s) spaced at regular intervals along their length (Passerieux et al 2006). The PJP’s are attached to the sarcolemma and transfer tensional forces between them through specific transmembrane proteins such as integrins, which interact with the inner cytoskeleton and contribute to the mechanosensing and regulatory abilities of each cell (Wang et al 2009; Brown et al 2012; Ingber et al 2014).
The points of intersection between these oriented collagen fibres then give rise to branching plexuses that ultimately connect to the surface of adjacent myofibres (and their endomysium) through perimysial junctional plates (PJP’s) spaced at regular intervals along their length (Passerieux et al 2006). The PJP’s are attached to the sarcolemma and transfer tensional forces between them through specific transmembrane proteins such as integrins, which interact with the inner cytoskeleton and contribute to the mechanosensing and regulatory abilities of each cell (Wang et al 2009; Brown et al 2012; Ingber et al 2014).
Although the tensile properties of the perimysium are similar to those of the endomysium, the fascicle ‘walls’ are much thicker and there is plenty of evidence to show that the perimysium is also involved in myofascial force transmission (Passerieux et al 2007; Purslow and Delage 2012 p 10), but a transfer of forces by trans-laminar shear within the shared walls of each fascicle seems improbable. Purslow and Delage (2012 p 8) explained that “deformations caused by shear through its thickness would be of orders of magnitude greater than in the endomysium, and so perimysium would represent a rather sloppy and inefficient force transmission pathway at physiologically-relevant muscle lengths.”
Schmalbruch (1985) cites an earlier model proposed by Feneis (1935) where the perimysium provides “neutral” connections between adjacent fascicles and enables them to slide past each other and facilitate changes in muscle shape during contraction (Purslow 2010). As all fan-shaped, fusiform and pennate muscles increase in width when contracting (Lieber and Friden 2000; Azizi et al 2008), any consequent changes in the angle that myofibres make with their tendinous/aponeurotic connections at either end (< 34o in human gastrocnemius muscle, Kawakami et al 1998) means that some sort of sliding element within the muscle is necessary in order to accommodate this (Purslow 2002) (figure 4). Purslow (1989) found that collagen fibres lie within the plane of the crossed-ply perimysial layers and do not run through the thickness of the inter-fascicular walls, which supports the model whereby the septal walls between adjacent fascicles can act as “neutral displacement membranes” that facilitate sliding during changes in shape (Feneis 1935; Schmalbruch 1985).
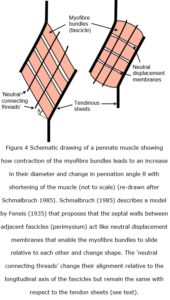 In the example given (figure 4) the muscle fibres and tendon sheets form a parallelogram, with the length of the myofibres being 60-70 % of the muscle belly length, so that shortening the myofibres shortens the muscle by about 33% and increases the collective diameters of the myofibre bundles (fascicles) by about 20% (Schmalbruch 1985). As muscles maintain a constant volume during contraction, so the cross-sectional area of the muscle fibres must increase, and similar changes in fascicle length have also been observed more recently in human gastrocnemius (38-25 mm, a change of 34%) (Kawakami et al 1998) and other muscles (Fukunaga et al 1997; Purslow 2002).
In the example given (figure 4) the muscle fibres and tendon sheets form a parallelogram, with the length of the myofibres being 60-70 % of the muscle belly length, so that shortening the myofibres shortens the muscle by about 33% and increases the collective diameters of the myofibre bundles (fascicles) by about 20% (Schmalbruch 1985). As muscles maintain a constant volume during contraction, so the cross-sectional area of the muscle fibres must increase, and similar changes in fascicle length have also been observed more recently in human gastrocnemius (38-25 mm, a change of 34%) (Kawakami et al 1998) and other muscles (Fukunaga et al 1997; Purslow 2002).
Azizi et al (2008) showed that changes in the pennate angle of muscle fibres (wild turkey) “decrease a muscle’s output force but increase output velocity by allowing the muscle to function at a higher gear ratio (muscle velocity/fiber velocity)”, and that “muscle-shape changes act as an automatic transmission system allowing a pennate muscle to shift from a high gear [1:1.4] during rapid contractions to low gear [1:1] during forceful contractions”, thus modulating muscle performance during mechanically diverse functions. However, their use of the term “rotation” to describe these changes in orientation of contracting myofibres (figure 4) is perhaps unfortunate as any perceived axis of rotation is a virtual contrivance.
While Schmalbruch’s (1985) description of Feneis’ (1935) model also includes “neutral connecting threads” that cross multiple perimysial fascicles as “large collagen bundles… arranged parallel to the tendons and obliquely to the muscle fibres… and hence do not resist movement of the fascicles”, so the alignment of these threads in this example (figure 4) suggest that these fibres may actually be part of the epimysium (see below).
Epimysium
The epimysium is an even thicker myofascial tissue that covers the entire muscle and is continuous with the perimysium lying beneath, and tendons at either end, as well as other fascial structures that surround it (Turrina et al 2013) (figure 1). Collagen cables of type I fibres are also crimped and even larger in diameter and generally form the same crossed-ply arrangement in resting fusiform muscles of ± 55o relative to the myofibre axis (Purslow 2010; Gillies and Lieder 2011). However, the myofibres within pennate muscles are themselves arranged at an angle to the collective direction of tension generation, and the arrangement of collagen fibres within these and some other muscles can be parallel to the long axis and form a dense surface layer that functions as a surface tendon (Benjamin 2009; Purslow 2010).
The main functions of the epimysium are thus the transmission of tensional forces (Huijing 2012b; Turrina et al 2013) and containment of the muscle during contraction (Passerieux et al 2007), but high levels of hyaluronic acid associated with proteoglycans in the outer epimysial layers also enable the muscle surface to slide with respect to adjacent structures (McCombe et al 2001). Although some epimysial surfaces are tightly bound to the deep fascia, the sliding ability of many others is facilitated by thin septal sheets and interposed loose connective tissues, which enable the muscle and surrounding tissues to accommodate to the changes in shape that occur during contraction (Stecco and Stecco 2012 a & b). However, it may be that this ‘sliding’ is at least partly due to structural rearrangements within mutually linked collagen fibres and proteoglycans at both ‘fibrillar’ and molecular levels, and related to the microvacuolar system described by Guimberteau (2005 & 2012); and ‘shear-linkage’ type connections of the endomysium (Purslow 2002) rather than a true shear (Levin and Martin 2012 p 139).
Although the myofascia has been classified into these distinct regions for the purpose of description, the structural complexity that unites them all into a functional unit also enables the efficient transfer of tensional force to other fascial tissues that surround the epimysium (Maas and Sandercock 2010; Huijing 2012b).
The fascial tissues associated with muscle
These include the inter-muscular fascial septa that connect adjacent muscles within a group; and the extra-muscular fasciae that merge with the deep fascia (fascia profunda), interosseal membranes and periosteum, and the neurovascular sheaths that enclose the nerves and vessels supplying the muscle (figure 1b). The deep, or ‘investing’, fascia is a tough tissue that surrounds and contains groups of muscles (compartments) and is continuous with aponeuroses (Mcombe et al 2001; Stecco and Stecco 2012a & b) and the overlying ‘superficial’ fascia that lies beneath the skin (Benjamin 2009; Abu-Hijleh et al 2012); and all are involved in the transfer of tension (Maas and Sandercock 2010; Huijing 2012b), with the loose fibre network of the superficial layer contributing to its flexibility (Iatridis et al 2003).
The distinctions between these different types of fascia can thus be rather tenuous at the microscopic level, as they are interlinked with each other, and the same named tissue can vary in its structural organization and functionality depending on where it appears in the body (Benjamin 2009; Stecco and Stecco 2012a & b). While collagen fibre alignments in the deep fascia have been noted as lying parallel with the muscles (McCombe et al 2001; Benjamin 2009), Benetazzo et al (2011) noted the mean angle between crossed-fibre orientations in human thoraco-lumbar and crural fascia as 78o, which indicates an average fibre angle of 39o relative to the body axis.
The helical tube
 All these tissues contribute to the highly complex and continuous structural network that extends from the inner cellular cytoskeleton, plasma membrane, endomysial sheath, perimysial fascicules and epimysium to the tendons and surrounding fascia, muscles and bone; with each region playing its own specialized part in the transfer of tension. The descriptions of myofascial tissues as ‘tubes’ naturally follows from their cross-sectional appearances; and the higher-level fascial tubes surrounding groups of muscles, the entire limb and body wall are similar (figures 1 & 2), with the orientations of collagen fibres within their walls having an important functional role.
All these tissues contribute to the highly complex and continuous structural network that extends from the inner cellular cytoskeleton, plasma membrane, endomysial sheath, perimysial fascicules and epimysium to the tendons and surrounding fascia, muscles and bone; with each region playing its own specialized part in the transfer of tension. The descriptions of myofascial tissues as ‘tubes’ naturally follows from their cross-sectional appearances; and the higher-level fascial tubes surrounding groups of muscles, the entire limb and body wall are similar (figures 1 & 2), with the orientations of collagen fibres within their walls having an important functional role.
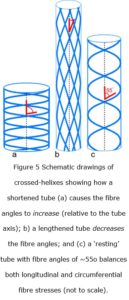
The ‘walls’ of the perimysium and epimysium are distinct in that they frequently contain two crossed-ply sets of collagen cables aligned at about ± 55o (relative to the long axis in resting fusiform muscles) (figure 3), while the apparently isotropic orientation of collagen fibres within the endomysium appears to be random but collectively has a (numbers-weighted) mean alignment of about 59o (Purslow and Trotter 1994). All these angles increase with muscle contraction and become more aligned with its transverse, or circumferential, plane and when the muscle is stretched the angles decrease as the fibres become aligned towards the main direction of tension, indicating that the collagen fibres are mechanically linked with each other (Purslow 1989; Chaudhry et al 2012). The particular alignments of collagen fibres within the walls of these tubes can thus not be considered incidental but a contributor to the mechanics of muscle function, which can be simply analysed if the crossed-ply sets of collagen are considered as left- and right-handed helixes, or spirals (figure 5).
CROSSED-PLY HELIXES
In 1958, Clarke and Cowey showed that changes in the relative length and diameter of certain nemertean and turbellarian worms were controlled by the particular alignment and geometric configuration of tensioned fibres within their body walls. 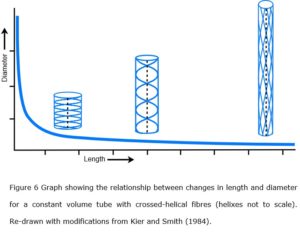 In essence, the inextensible fibres were constrained by the crossed-helical geometry surrounding the pressurized body tube and enabled it to maintain a constant volume throughout changes in shape; and this basic hydrostatic model has now become entrenched as a design principle in biomechanics (Wainwright 1988; Shadwick 2008; Kier 2012).
In essence, the inextensible fibres were constrained by the crossed-helical geometry surrounding the pressurized body tube and enabled it to maintain a constant volume throughout changes in shape; and this basic hydrostatic model has now become entrenched as a design principle in biomechanics (Wainwright 1988; Shadwick 2008; Kier 2012).
A crossed-helical tube that is shortened will cause the fibre angles to increase (relative to the tube axis) while one that is extended in length will cause them to decrease; and in both cases, the tension within the fibres becomes greater as the tube shape moves away from its central resting position (Purslow 1989; Goriely and Tabor 2013)(figure 6). The optimum shape that balances both longitudinal and circumferential stresses is when the fibres are at an angle of ~55o, i.e. these fibre orientations are reflecting the most efficient distribution of mechanical stresses and coordinating the changes in shape of the tube, as well as providing a system of elastic energy storage that assists in returning the tube to its resting state (figure 6) (Clarke & Cowey 1958).
The muscular tube
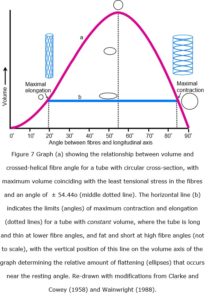 The tensioned fibres actually follow the course of geodesics, or the shortest line between two points on the surface of a curve, and the theoretical relationship between fibre angle and volume is relatively simple for a tube with circular cross-section (figure 7a). Muscles, however, maintain an almost constant volume during contraction and elongation, with Baskin & Paolini (1966) finding variations in frog sartorius muscle of less than 0.006 cm3 per 100 g of muscle (Rana, ex-vivo), but the graph is still relevant if the cross-section of the tube is an ellipse, or non-circular, where changes in the fibre-angle follow a horizontal line (b) within the boundaries of the curve (a) (Clarke and Cowey 1958).
The tensioned fibres actually follow the course of geodesics, or the shortest line between two points on the surface of a curve, and the theoretical relationship between fibre angle and volume is relatively simple for a tube with circular cross-section (figure 7a). Muscles, however, maintain an almost constant volume during contraction and elongation, with Baskin & Paolini (1966) finding variations in frog sartorius muscle of less than 0.006 cm3 per 100 g of muscle (Rana, ex-vivo), but the graph is still relevant if the cross-section of the tube is an ellipse, or non-circular, where changes in the fibre-angle follow a horizontal line (b) within the boundaries of the curve (a) (Clarke and Cowey 1958).
Such a tube would only have a circular cross-section when it reached either of these two extremes, i.e. when the fibres are under the greatest amount of tensional stress, with the tube progressively flattening towards the middle as the fibre angles approach 54.44o; the angle where tension is at a minimum, and circumferential and longitudinal stresses are balanced (Clarke and Cowey 1958).
The constraining fibres
It should be recognized that the apparently continuous collagen fibers that stretch between the ends of the crossed-helical tubes shown in figures 5 – 7 are really graphic representations of bundles of shorter collagen molecules/fibrils that are cross-linked together and transfer tensional forces between them (Avery and Bailey 2008; Purslow 2010).
Muscles generally have an elliptical or irregular cross-section with considerable variation in shape in-vivo (figure 1b) and normally operate in the near-horizontal part of the curve shown in figure 6 and middle region of the horizontal line in figure 7b and rarely, if ever, reach the extremes of shape and fibre alignment shown (Purslow 1989). It is thus important to note that the ideal curves shown in these figures are theoretical representations of the mechanical behaviour of crossed-helical tubes with inextensible fibres, while the wavy crimped collagen fibres in the perimysium and epimysium (figure 3) can be stretched by an additional five per cent of their length; and such tubes are likely to behave differently (Clarke and Cowey 1958).
Purslow (1989) showed that the crimp angle (~ 39o in resting muscle) contributes to the elasticity of individual fibres and that this angle decreases (as tension in the fibres increases) and they are straightened out during changes in muscle length and shape. A correlation with changes in sarcomere length (fusiform muscle in vitro) and crossed-helical fibre angles (1.1µm at ~20o to 3.9µm at ~80o) confirmed that the straightened fibres are acting as constraints to further increases in muscle length and circumference, and that these particular angles corresponded with a sudden and dramatic increase in the stiffness (0 – ~18 KPa) and ability of the perimysium to transfer significant tensional forces (Purslow 1989). However, these extremes are well beyond the normal range of living muscle, which explains why they can change shape with ease.
Variations in angle
Variations in the resting fibre angles of a collagen-reinforced tube would undoubtedly depend on its particular functional activities, such as in bovine semitendinosus muscle where collagen fibres are generally aligned parallel (0o) to the long axis and cause it to act more as an epitendon (Purslow 2010), and in the deep fascia where they can be arranged similarly (McCombe et al 2001; Benjamin 2009). While the arrangement of collagen fibres within the epimysium of pennate muscles may be “parallel to the long axis of the muscle and forms a dense surface layer that functions as a surface tendon” (Purslow 2010), the myofibres are arranged at an angle to this, and there is some gradation in collagen fibre angle as the myofascia transits into functionally related tissues with different mechanical properties. Passerieux et al (2007) showed that oblique perimysial fibres become more axially aligned with the overall direction of muscle tension generation as they approach the myotendinous junction (bovine flexor carpi radialis). Tendons, however, are more complicated than is generally recognized, with collagen fibres tending to form complex plaits and spirals in both longitudinal and transverse directions (Kannus 2000); and in ligaments, their complex myofascial connections and variable internal organization suggest a much more complex multi-axial loading (Van der Wal 2009).
A ubiquitous pattern
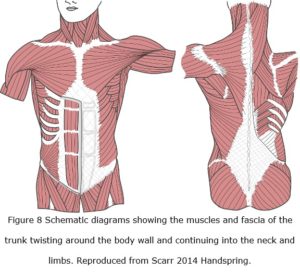 Crossed-helical winding and its functional significance have been described in the body walls of squid (Johnsen & Kier 1993), amphibians (O’Reilly et al 2000), eels (Hebrank 1980), fish, dolphins and whales (Pabst 2000) suggesting that a similar pattern is likely to occur throughout the human. Indeed, the alignments of muscle and investing fascial tissues that curve around the body wall and limbs are also suggestive of helical arrangements, if only in part (Benetazzo et al 2011; Vleeming 2012) (figure 8); and Scarr (2013) also suggested an alternative helical arrangement of collagen in the limbs of mammals, although this remains unconfirmed.
Crossed-helical winding and its functional significance have been described in the body walls of squid (Johnsen & Kier 1993), amphibians (O’Reilly et al 2000), eels (Hebrank 1980), fish, dolphins and whales (Pabst 2000) suggesting that a similar pattern is likely to occur throughout the human. Indeed, the alignments of muscle and investing fascial tissues that curve around the body wall and limbs are also suggestive of helical arrangements, if only in part (Benetazzo et al 2011; Vleeming 2012) (figure 8); and Scarr (2013) also suggested an alternative helical arrangement of collagen in the limbs of mammals, although this remains unconfirmed.
Crossed-helical arrangements of collagen have also been described in the walls of elastic arteries (Holzapfel 2006), the inter-vertebral disc (Hukins and Meakin 2000), heart (Buckberg 2002), trachea, oesophagus (Carey 1920a & b), small intestines (Gabella 1987) and embryonic notochord (Koehl et al 2000); and tubular organs that maintain constant volume throughout changes in shape due to crossed-helical arrangements of muscle and fascial tissue have also been described in the tongues of mammals and lizards, the arms and tentacles of cephalopods and the trunks of elephants (Kier & Smith 1985). The mechanical principles that underlie the value of this ubiquitous pattern in biology even contribute to the novelty of the ‘Chinese finger trap’ toy and its effectiveness as a suture in gastro-intestinal surgery (Song et al 2008).
Considering the similarity between the theoretical fibre angle that balances both longitudinal and circumferential stresses (54.44o), and the alignment of collagen fibres within the myofascia of resting muscles and other biological examples, it would seem that these geometric crossed-helical arrangements are indeed contributing to the coordination of changes in muscle shape. They would also enable such tubes to bend smoothly without kinking and resist torsional deformations, thus further demonstrating the value of this particular arrangement to muscle mechanics (Wainwright 1988 p 71; Etnier 2003).
DISCUSSION
Although collagen fibre angles quoted in the literature are sometimes stated in relation to the transverse axis they have been converted here relative to the longitudinal axis of the tube for comparison purposes. Biological helixes are not continuous, like metal springs, but consist of multiple discrete components (fibres) arranged into these particular geometric configurations because they are the most efficient packing arrangement within a dynamic environment (Pickett et al 2000). The orientation of fibres with respect to the longitudinal axis then distinguishes this biological configuration from the continuous ‘helical angle’ that is perpendicular to it and as used in mechanical engineering.
Simple hydrostat or integrated structure?
Crossed-helical configurations in biological tissues are widely considered to be acting as hydrostats (Wainwright 1988; Aspden 1990; Kier 2012; Goriely and Tabor 2013; Findley et al 2015), where an incompressible fluid contained within a tube is constrained by tensioned fibres in the tube wall, but this seems to be far too simplistic on its own when considering the high level of structural organization within muscle (Levin 2014). Although an increase in intra-muscular pressure as the result of lateral tissue constraint would increase muscle stiffness and lead to increased force production during active contraction (Purslow 2002), muscles are not like pressurized balloons (Levin 2002; Sharkey 2015) and most of the water contained within them is tightly bound to a wide diversity of proteoglycan complexes that are cross-linked with the collagen fibres (Gillies and Lieber 2011).
While the measurement of normal intra-muscular pressures during contraction (15 – 141 mm Hg) is notoriously difficult (Hill 1948; Ward et al 2007; Aweid et al 2012), pressures of 6 – 12 mm Hg at rest (Aweid et al 2012) may be at least partly due to the passive muscle stiffness, or intrinsic tension, that naturally occurs in muscle tissues in-vivo (Schleip et al 2006; Masi and Haanon 2010).
Collagens are the main tension-bearing element within ECM/fascial tissues and are aligned parallel to the local tissue strain (Purslow 2010) with the cells contained within them also contributing to this tension (Tomasek et al 2002). Myofibroblasts generate significant tensional forces due to the presence of smooth muscle-like actin filaments within their cytoskeletons and transfer this into the surrounding ECM through transmembrane proteins, and they play an important role in tissue contracture during wound healing and other fascial pathologies (Tomasek et al 2002). This contractile ability thus enables myofibroblasts to contribute to the intrinsic tension/passive stiffness of muscle and other tissues (Schleip et al 2006), and perhaps even assist in organizing or fine-tuning the crossed-helical lattice as the most efficient distribution of tension. So, while it has been assumed that the walls containing these crossed-helical arrangements simply apply pressure against the contents of a fluid filled bag during changes in shape, a more complex picture emerges.
A new model
The contraction of myofibres mechanically influences the endomysium, perimysium and epimysium (as described above) and leads to shortening of the entire muscle because of their tensional continuity with each other and the tendinous tissues at each end (figures 5).While the walls of these tubes have been widely considered as compressing the contents of a constant-volume tube, they are already under tension, and the collagen and proteoglycans molecules within them are mechanically linked with each other (Wess 2008).
It has thus been suggested that structural rearrangements, and moment by moment changes in the balance between tensioned collagen fibres and compressed proteoglycans at both fibrillar and molecular levels, and across the myofascial hierarchy, also regulate the changes in shape of muscle and that perhaps an equivalent mechanism operates within the tubular hierarchy of surrounding fascial tissues (Levin 2014). This balance between tension and compression acting within and between different tissues has been considered in relation to tensegrity, a structural design principle whose significance is increasingly recognized in structural biology, but the reader is referred elsewhere for further information (Levin 2002; Ingber et al 2014; Scarr 2014).
A brief summary
The endomysial sheath (tube) surrounding each myofibre is shared with those adjacent to it and transmits the force of contraction through trans-laminar ‘shear’, and ultimately to the tendinous tissues at either end of the muscle; and because this network forms a tight and seamless connection that is continuous across the whole fascicle, its behaviour is transversely isotropic to changes in shape (Purslow and Trotter 1994; Chaudhry et al 2012). The perimysium also forms a honey-comb like network (at a higher size-scale) that extends across the entire muscle and continues into the epimysium, with the larger fascicles giving rise to smaller fascicles that subdivide into successively smaller bundles and ultimately connect to the endomysium and individual myofibres (Passerieux et al 2006; Purslow 2010). However, the transverse anisotropy of this perimysial network suggests that changes in muscle diameter will not be the same in every direction (Sharafi and Blemker 2010), thus complicating the precise relationship between muscle length and diameter during changes in shape. Although Schmalbruch’s (1985) description of the Feneis (1935) model includes “neutral displacement membranes” within the walls of adjacent perimysial sheets, and which enable the fascicles to slide against each other during changes in muscle shape (figure 4), confirmation of the details of this mechanism are still needed.
Bundles of collagen fibres within the perimysium and epimysium form crossed-helical arrangements that balance and coordinate the longitudinal and circumferential stresses within the walls of these myofascial tubes during changes in muscle shape; but more comparative details of their alignments within fusiform, fan-shaped and pennate muscles are needed. Myofascial hierarchies are interconnected and extremely complex, and much information has been determined on two-dimensional tissue samples, with relatively few attempts made to extrapolate them to the behaviour of crossed-helical tubes; and although this tubular perspective is itself a simplification, much is likely to be gained from an understanding of these geometric patterns.
CONCLUSION
Helixes spontaneously appear in self-organizing systems as the most efficient way of organizing components of similar size on the surface of a cylinder or tube (Pickett et al 2000). They are a common motif in protein construction because they provide an energy-efficient solution to molecular close-packing (Snir & Kamien 2005) and form a structural model for coiled winding at multiple size scales throughout the body (Scarr 2011) and in a diverse group of organisms (Kier and Smith 1985). The formation of a helix is based on simple geometric principles (Sadoc & Rivier 2000; Pickett et al 2000; Lord 2002) and its persistence is ensured because it is one of the most stable of structural configurations. It is thus not surprising that a system of crossed-helical tubes should predominate in compliant biological tissues because this is one of the most efficient ways of optimizing mechanical stresses within their walls (Clarke and Cowey 1958; Wainwright 1988; Kier 2012).
The myofascia, as a fibrous specialization of fascial/ECM tissues that surround and interpenetrate muscles is then a complex hierarchy of helically-reinforced tubes contained within larger tubes; and continuous with higher-level fascial tubes that surround groups of muscles, the limbs and entire body (figures 1 & 2). Bundles of collagen fibres within the perimysium and epimysium form crossed-helical configurations (figure 3) that balance longitudinal and circumferential stresses and coordinate changes in muscle shape during contraction and extension (figures 4 – 7), and should thus be considered as an essential part of muscle function.
ACKNOWLEDGEMENTS
I would like to thank Stephen Levin for his views on the standard muscular hydrostat model and for questioning whether a true shear (rather than an apparent one) really occurs within normally functioning tissues; also to the anonymous reviewer who rigorously questioned the assumptions made and provided much-needed food for thought.
REFERENCES
Abu-Hijleh M, Dharap AS, Harris PF 2012 Fascia superficialis. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh 19-23.
Aaron JE 2012 Periosteal Sharpey’s fibers: a novel bone matrix regulatory system. Frontiers in Endocrinology 3: 1-10.
Aspden RM 1990 Constraining the lateral dimensions of uniaxially loaded materials increases the calculated strength and stiffness: application to muscle and bone. Journal of Materials Science: Materials in Medicine I: 100-104.
Avery NC, Bailey AJ 2008 Restraining cross-links responsible for the mechanical properties of collagen fibers: natural and artificial. In: Fratzl P (ed) Collagen: structure and mechanics. Springer, New York; 81-110.
Aweid O, Del Buono A, Malliaras P, Iqbal H, Morrissey D, Maffulli N, Padhiar N 2012 Systematic review and recommendations for intracompartmental pressure monitoring in diagnosing chronic exertional compartment syndrome of the leg. Clinical Journal of Sports Medicine 22: 356-370.
Azizi E, Brainerd EL, Roberts TJ 2008 Variable gearing in pennate muscles. Proceedings of the National Academy of Sciences 105: 1745-1750.
Baskin RJ, Paolini PJ 1966 Muscle volume changes. Journal of General Physiology 49: 387-404.
Benetazzo L, Bizzego A, De Caro R, Frigo G, Guidolin D, Stecco C 2011 3D reconstruction of the crural and thoracolumbar fasciae. Surgical and Radiologic Anatomy 33: 855-862.
Benjamin M 2009 The fascia of the limbs and back – a review. Journal of Anatomy 214: 1-18.
Brown SC, Mueller U, Conti FJ 2012 Integrins in the development and pathology of skeletal muscle. In: Zaher A (ed) Neuromuscular disorders InTech 1-20.
Buckberg GD 2002 Basic science review: the helix and the heart. Journal of Thoracic and Cardiovascular Surgery 124:863-883.
Carey EJ 1920 Studies in the dynamics of histogenesis: I. Tension of differential growth as a stimulus to myogenesis. Journal of General Physiology 2: 357-372.
Carey EJ 1920 Studies in the dynamics of histogenesis: II. Tension of differential growth as a stimulus to myogenesis in the esophagus. Journal of General Physiology 3: 61-83.
Chaudhry H, Max R, Stecco A, Findley T 2012 Mathematical model of fiber orientation in anisotropic fascia layers at large displacements. Journal of Bodywork and Movement Therapies 16: 158-164.
Clark RB, Cowey JB 1958 Factors controlling the change of shape of certain nemertean and turbellarian worms. Journal of Experimental Biology 35: 731-748.
Etnier SA 2003 Twisting and bending of biological beams: distribution of biological beams in a stiffness mechanospace. The Biological Bulletin 205: 36-46.
Feneis H 1935 Uber die anordnung und die bedentung des indegewebes für die mechanik der skelettmuskulatur. Morph Jb 76: 161-202.
Findley TW, Shalwala M 2013 Fascia research congress evidence from the 100 hundred year perspective of Andrew Taylor Still. Journal of Bodywork and Movement Therapies 17: 356-364.
Findley T, Chaudhry H, Dhar S 2015a Transmission of muscle force to fascia during exercise. Journal of Bodywork and Movement Therapies 19:119-123.
Fukunaga T, Ichinose Y, Ito M, Kawakami Y, Fukashiro S 1997 Determination of fascicle length and pennation in a contracting human muscle in vivo. Journal of Applied Physiology 82: 354-358.
Gabella G 1987 The cross-ply arrangement of collagen fibres in the submucosa of the mammalian small intestine. Cell and Tissue Research 248: 491-497.
Gaunt AS, Gans C 1992 Serially arranged myofibres: an unappreciated variant in muscle architecture. Muscle and Nerve 44: 318-331.
Gillies AR, Lieber RL 2011 Structure and function of the skeletal muscle extracellular matrix. Muscle and Nerve 44: 318-313.
Goriely A, Tabor M 2013 Rotation, inversion and perversion in anisotropic elastic cylindrical tubes and membranes. Proceedings of the Royal Society A 469: 20130011.
Guimberteau JC 2005 The sliding mechanics of the subcutaneous structures in man, illustration of a functional unit: the microvacuoles. Studies of the Académie Nationale de Chirurgie 4: 35-42.
Guimberteau JC 2012 The subcutaneous and epitendinous tissue behaviour of the multimicrovacuolar sliding system. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh 143-146 & plates 3.6.1-6.
Hebrank MR 1980 Mechanical properties and locomotor functions of eel skin. Biological Bulletin 158: 58-68.
Hill AV 1948 The pressure developed in muscle during contraction. Journal of Physiology 107: 518-526.
Holzapfel GA 2006 Determination of material models for arterial walls from uniaxial extension tests and histological structure. Journal of Theoretical Biology 238: 290-302.
Huijing PA 2012a Force transmission and muscle mechanics. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh pp 113-115.
Huijing PA 2012b Myofascial force transmission. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh pp 117-122.
Hukins DWL, Meakin JR 2000 Relationship between structure and mechanical function of the tissues of the intervertebral joint. American Zoologist 40: 42-52.
Iatridis JC, Wu J, Yandow JA, Langevin HM 2003 Subcutaneous tissue mechanical behaviour is linear and viscoelastic under uniaxial tension. Connective Tissue Research 44: 208-217.
Ingber DE, Wang N, Stamenovic D 2014 Tensegrity, cellular biophysics and the mechanics of living systems. Reports on Progress in Physics 77: 046603.
Johnsen S, Kier WM 1993 Intramuscular crossed connective tissue fibres: skeletal support in the lateral fins of squid and cuttlefish (Mollusca: Cephalopoda). 231: 311-338.
Kannus P 2000 Structure of the tendon connective tissue. Scandinavian Journal of Medicine and Science in Sports 10: 312-320.
Kawakami Y, Ichinose Y, Fukunaga T 1998 Architectural and functional features of human triceps sure muscles during contraction. Journal of Applied Physiology 85: 398-404.
Kier WM, Smith KK 1985 Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrostats. Zoological Journal of the Linnean Society 83: 307-324.
Kier WM 2012 The diversity of hydrostatic skeletons. Journal of Experimental Biology 215: 1247-1257.
Koehl MAR, Quillin KJ, Pell CA 2000 Mechanical design of fiber-wound hydraulic skeletons: the stiffening and straightening of embryonic notochords. American Zoologist 40: 28-41.
Lieber RL and Fridén J 2000 Functional and clinical significance of skeletal muscle architecture. Muscle and Nerve 23: 1647-1666.
Levin SM 2002 The tensegrity truss as a model for spine mechanics: biotensegrity. Journal of Mechanics and Medicine in Biology 2: 375-378.
Levin SM 2014 Personal Communication.
Levin SM and Martin DC 2012 In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh 137-142.
Lord EA 2002 Helical structures: the geometry of protein helices and nanotubes. Structural Chemistry 13: 305-314.
Maas H, Sandercock TG 2010 Force transmission between synergistic skeletal muscles through connective tissue linkages. Journal of Biomedicine and Biotechnology 2010: 575672 doi:10.1155/2010/575672.
Masi AT, Hannon JC 2008 Human resting muscle tone (HRMT): narrative introduction and modern concepts. Journal of Bodywork and Movement Therapies 12: 320-332.
McCombe D, Brown T, Slavin J, Morrison WA 2001 The histochemical structure of the deep fascia and its structural response to surgery. Journal of Hand Surgery (British and European Volume 26B: 89-97.
Meyer GA, Lieber RL 2011 Elucidation of extracellular matrix mechanics from muscle fibers and fiber bundles. Journal of Biomechanics 44:771-773.
Nishimura T, Ojima K, Liu A, Hattori A, Takahashi K 1996 Structural changes in the intramuscular connective tissue during development of bovine semitendinosus muscle. Tissue and Cell 28: 527-536.
O’Reilly J.C, Rittert DA, Carrier DR 1997 Hydrostatic locomotion in a limbless tetrapod. Nature 386: 269-272.
Pabst DA 2000 To bend a dolphin: convergence of force transmission designs in Cetaceans and Scombrid fishes. American Zoologist 40: 146-155.
Passerieux E, Rossignol R, Chopard A, Carnino A, Marini JF, Letellier T, Delage JP 2006 Structural organization of the perimysium in bovine skeletal muscle: junctional plates and associated intracellular subdomains. Journal of Structural Biology 154: 206-216.
Passerieux E, Rossignol R, Letellier T, Delage JP 2007 Physical continuity of the perimysium from myofibers to tendons: involvement in lateral force transmission in skeletal muscle. Journal of Structural Biology 159: 19-28.
Pickett GT, Gross M, Okuyama H 2000 Spontaneous chirality in simple systems. Physical Review Letters 85: 3652-3655
Purslow PP 1989 Strain-induced reorientation of an intramuscular connective tissue network: implications for passive muscle elasticity. Journal of Biomechanics 22: 21-31.
Purslow PP 2002 The structure and functional significance of variations in the connective tissue within muscle. Comparative Biochemistry and Physiology Part A 133: 947-966.
Purslow PP 2010 Muscle fascia and force transmission. Journal of Bodywork and Movement Therapies 14: 411-417.
Purslow PP, Delage JP 2012 General anatomy of the muscle fascia. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 5-10.
Purslow PP, Trotter JA 1994 The morphology and mechanical properties of endomysium in series-fibred muscles: variations with muscle length. Journal of Muscle Research and Cell Motility 15: 299-308.
Rowe RWD 1981 Morphology of perimysial and endomysial connective tissue in skeletal muscle. 13: 681-690.>
Sadoc JF, Rivier N. 2000 Boerdijk-Coxeter helix and biological helices as quasicrystals. Materials Science and Engineering A 294-296: 397-400.>
Scarr G 2011 Helical tensegrity as a structural mechanism in human anatomy. International Journal of Osteopathic Medicine 14: 24-32.
Scarr G 2013 Palpatory phenomena in the limbs: a proposed mechanism. International Journal of Osteopathic Medicine 16: 114-120.
Scarr G 2014 Biotensegrity: the structural basis of life. Handspring Edinburgh.
Schleip R, Naylor IL, Ursu D, Melzer W, Zorn A, Wilke HJ, Lehmann-Horn F, Klingler W 2006 Passive muscle stiffness may be influenced by active contractility of intramuscular connective tissue. Medical Hypotheses 66: 66-71.
Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh.
Schmalbruch H 1985 Skeletal muscle. Springer Berlin; pp14-22.
Shadwick RE 2008 Foundations of animal hydraulics: geodesic fibres control the shape of soft bodied animals. Journal of Experimental Biology 211: 289-291.
Sharafi B, Blemker SS 2010 A micromechanical model of skeletal muscle to explore the effects of fiber and fascicle geometry. Journal of Biomechanics 3207-3213.
Sharafi B, Blemker SS 2011 A mathematical model of force transmission from intrafascicularly terminating muscle fibers. Journal of Biomechanics 44: 2031-2039.
Sharkey J 2015 Letter to the Editor re: [Findley T, Chaudhry H, Dhar S 2015 Transmission of muscle force to fascia during exercise. Journal of Bodywork and Movement Therapies 19:119-123]. Journal of Bodywork and Movement Therapies 19: 391.
Snir Y, Kamien RD 2005 Entropically driven helix formation Science 307: 1067.
Song EK, Mann FA, Wagner-Mann CC 2008 Comparison of different tube materials and use of Chinese finger trap or four friction suture technique for securing gastrostomy, jejunostomy and thoracostomy tubes in dogs. Veterinary Surgery 37: 212-221.
Stecco C, Stecco A 2012 Deep fascia of the shoulder and arm. Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 25-29.
Stecco C, Stecco A 2012 Deep fascia of the lower limbs. Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 31-35.
Still AT 1899 Philosophy of osteopathy. Self-published Kirksville MO.
Tomasek JJ, Gabbiani G, Hinz B, Chaponnier C, Brown RA 2002 Myofibroblasts and mechano-regulation of connective tissue remodelling. Nature Reviews 3: 349-363.
Trotter JA, Purslow PP 1992 Functional morphology of the endomysium in series fibered muscles. Journal of Morphology 212: 109-122
Turrina A, Martinez-González MA, Stecco C 2013 The muscular force transmission system: role of the intramuscular connective tissue. Journal of Bodywork and Movement Therapies 17: 95-102.
Van der Wal J 2009 The architecture of the connective tissue in the musculoskeletal system – an often overlooked functional parameter as to proprioception in the locomotor apparatus. International Journal of Therapeutic Massage and Bodywork 2: 9-23.
Vleeming A 2012 The thoracolumbar fascia: an integrated functional view of the anatomy of the TLF and coupled structures. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 37-43.
Wainwright SA 1988 Axis and circumference: the cylindrical shape of plants and animals. Harvard University Press, Cambridge.
Wang N, Tytell JD, Ingber DE 2009 Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nature Reviews 10: 75-82.
Ward SR, Davis J, Kaufman KR, Lieber RL 2007 Relationship between muscle stress and intramuscular pressure during dynamic muscle contractions. Muscle & Nerve 36: 313-319.
Wess TJ 2008 Collagen fibrillar structure and hierarchies. In: Fratzl P ed. Collagen: structure and mechanics Springer, New York 49-80.
