PALPATORY PHENOMENA IN THE LIMBS: A PROPOSED MECHANISM

International Journal of Osteopathic Medicine

2013;16:114-120 ^link

Graham Scarr    ^{request copy}

KEYWORDS

Collagen; cranial osteopathy; cranio-sacral therapy; crossed-helix; Fibonacci; helix; myofascia; palpation; pangolin; primary respiratory mechanism.

ABSTRACT

Practitioners described as ‘cranial’ osteopaths and ‘cranio-sacral’ therapists routinely observe palpatory phenomena within the limbs of patients and use these findings to inform diagnosis and treatment. As current anatomical knowledge is unable to explain this, it is hypothesized that cyclic changes in vascular volume (Traube-Hering-Mayer waves) alter the tension in associated myofascia and create patterns of motion that are palpable. These particular patterns result from the helical alignment of collagen fibres and may be altered by pathologies, such as ‘repetitive strain injury’ (RSI) and ‘tennis elbow’, reverting to normal following successful treatment. Helixes spontaneously appear in self-organizing processes, and a comparison between different species suggests that the proposed pattern may be an intrinsic part of mammalian limb development. Confirmation of this mechanism requires more detailed examination of limb myofascia and could lead to wider acceptance of this particular mode of treatment.

INTRODUCTION

Practitioners described as ‘cranial’ osteopaths and ‘cranio-sacral’ therapists routinely observe palpatory phenomena within the limbs of their patients.¹ They report a sense of rhythmic expansion and contraction within the limbs, with varying amounts of rotation and length change,² and a probable amplitude within a few hundred microns. The directional pattern of motion is altered by pathologies such as ‘repetitive strain injury’ and ‘tennis elbow’, reverting to normal following treatment.

This information, however, is mostly anecdotal with no studies on efficacy in limb treatment and current anatomical knowledge unable to explain the directional bias in motion. Some writers consider the whole concept illusory and attribute any therapeutic benefit to placebo.^3,4 A mechanism that might explain these phenomena, based on a reassessment of the architectural geometry of fascial tissues, is proposed. It is hoped that this will stimulate further research into this modality of treatment.

The ‘cranial’ approach considers an involuntary mechanism, first described [in part] by Swedenborg during the eighteenth century⁵ and elaborated on by Sutherland (1939),⁶ whereby connective tissues in the body are subject to a cyclic change in tension and small amount of motion, typically from two to fourteen times a minute (0.03 – 0.23 Hz).⁷ Practitioners consider this to be part of normal physiology and the quality of motion an indicator of the ‘health’ or dysfunction of any particular tissue; Woods and Woods (1961) described the palpable sensation as the ‘cranial rhythmic impulse’ (CRI).⁸

Chaitow (1999)⁹ and Ferguson (2003)¹⁰ reviewed different driving mechanisms that have been proposed for this motion, most of which originate in the cranium and transfer through the fascia, or act peripherally through the nervous and vascular systems. Sutherland’s (1939)⁶ suggestion of inherent expansion and contraction of brain tissue was followed by a hydrostatic model, where fluctuations in the production and re-absorption of cerebrospinal fluid (CSF) cause periodic changes in intracranial volume, articular mobility of cranial bones and sacral mobility through meningeal connections.^11,12 Moskalenko et al (2009)¹³ extended this model to include changes in vascular tone within the brain that induce similar oscillations in intracranial pressure and outflow of CSF into the spinal cavity, but the precise origin of the mechanism remains unknown.

A key part of the ‘cranial’ concept is that bones of the skull remain distinct throughout life and have a rhythmic motion that is palpable as the CRI. This differs from the conventional view that considers sutures between the bones as merely accommodating brain growth and fusing in the third decade of life.^14,15 However, there is considerable variation in the pattern and timing of sutural fusion throughout life and ‘closed’ sutures frequently have little more than a mineralized veneer over their outer surface.¹⁶ Animal studies clearly demonstrate sutural patency throughout life, which suggests that complete fusion may be a semi-pathological state in humans. Recent data show that the growing infant brain does not push bones of the cranial vault outwards,¹⁸ as previously thought,¹⁴ and an alternative mechanism that allows the vault to retain a certain amount of structural and functional autonomy makes bone mobility feasible.¹⁹

Sutherland (1939)⁶ considered cranial bone motion to be one of five distinct ‘phenomena’ that includes mobility of the meninges and sacrum, motility of the brain, and fluctuation of the CSF within a ‘Primary Respiratory Mechanism’ (PRM). The term ‘PRM’ implies a fundamental relationship between the cranium, fascia and cellular respiration and places thoracic breathing as ‘secondary’.¹ It should be noted that the phenomena observed in the limbs are not the same as Sutherland’s ‘five phenomena’ but are probably part of the same entity. The CRI is the palpable manifestation of the PRM and is most evident on the head although recognizable on all parts of the body; it can be disturbed by trauma and pathology.^1,2,11,12

The PRM/CRI is a decidedly controversial aspect of osteopathic medicine. It is a subtle enough phenomenon to be easily overlooked by untrained clinicians… [which] has led many to doubt its existence” (Nelson et al 2001).²⁰ Green et al (1999)²¹ reviewed the evidence supporting the ‘cranial’ concept and found that experimental protocols and subsequent analyses were generally inadequate to justify the conclusions purported by their authors. However, Nelson et al (2001)²⁰ later measured cyclic changes in blood flow known as Traube-Hering-Mayer waves²² and demonstrated a statistically significant correlation with the CRI, while Moskalenko et al (2001)²³ found similar periodic movements of CSF based on oscillations of brain vessel tone. Christ et al (1995)²⁴ measured cyclic changes in limb volume within the CRI range and suggested that they were due to variations in arterial pressure, arteriolar vasomotion and possibly lymphatic diameter. A later review by Nelson (2011)⁷ concluded that ‘cranial’ manipulation has a significant affect on blood flow but that practitioners can recognize a variety of physiological frequencies, which may have contributed to earlier confusion regarding the precise CRI rate.²⁵ Karni et al (1983)²⁶ recognized that variations in vessel calibre might influence limb volume and relate to the palpable CRI, although the protocol and analysis are questionable;²¹ even so, rhythmic changes in fluid volume^7,20,24 might be responsible for the sense of limb expansion and contraction observed by practitioners.² To understand the mechanism that may explain these findings it is necessary to examine the microstructure of fascia.

THE MYOFASCIAL SHEATH

Originally considered as mere packing tissue, the fascia forms a continuous network throughout the body with hierarchical compartments of myofascia, or ‘tubes within tubes’, that are particularly noticeable in cross-sections of the limbs. A delicate network of endomysium surrounds individual muscle fibres and is continuous with the perimysium ensheathing groups of fibres in parallel bundles, or fasciculi. Perimysial septa are themselves inward extensions of the epimysium, which covers the muscle and is continuous with the superficial fascia investing whole muscle groups and skin.^27-29

Purslow and Trotter (1994)^30,31 found [in bovines] that peri- and epimysial sheaths are reinforced by two helical crossed-ply sets of collagen, with a mean resting fibre orientation of 55^o (relative to the muscle axis), while endomysial fibres are far more disordered but have a numbers-weighted average of 59^o.³⁰ Benetazzo et al (2011)³² noted the mean angle between crossed-fibre orientations in human thoraco-lumbar and crural fascia in the horizontal plane as 78^o, which indicates an average fibre angle of 51^o compared to the body/limb axis. As the overall fibre orientation directly influences how a helix responds to changes in length and volume^33,34 it is suggested that this correlates with the phenomena observed on palpation.

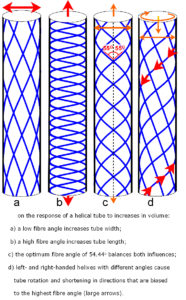A fibre orientation of 54.44^o (axial) is the optimal angle for balancing circumferential and longitudinal stresses in crossed-helixes (fig. 1c),^33,34 with a lower angle resisting tube elongation and a higher angle resisting circumferential increases.³⁵ As a cyclic increase in vascular volume leads to similar changes in limb volume,²⁴ a lower fibre angle would then be compatible with a sense of circumferential expansion on palpation (fig. 1a) and a higher angle with a sense of limb lengthening (fig. 1b). These two outcomes are possible because the collagen fibre angles in left and right-handed crossed-helixes are the same;^33,34 but what would happen if they differed?

Preliminary experiments on crossed-helixes with different angles show that an increase in volume causes rotation and shortening in a preferred direction, and that this follows fibres with the highest angle (fig. 1d)³⁶ (crossed-helixes with the same angle do not rotate because each helix counteracts the rotational influence of the other (fig. 1a-c)). Similarly, two palpable phases of the CRI cycle in the limbs are ‘expansion with external rotation and shortening’ (‘flexion’ phase) followed by ‘contraction with internal rotation and lengthening’ (‘extension’ phase),^1,2 i.e. helical motion. Even though practitioners may not recognize all these elements to the same extent, the normal palpable pattern and its variations can all be explained by a cyclic change in volume and the helical alignments of collagen in the myofascia; but what would cause the fibre angles to differ?

A helix is the most efficient packing arrangement of objects on the surface of a cylinder or tube^37,38 and a fundamental structural model in biology,³⁹ from plants⁴⁰ to the body walls of worms,³³ fish and dolphins.⁴¹ It is also a common motif in protein construction and a recognizable pattern throughout the human body, including the arterial wall,⁴² intervertebral disc,⁴³ and fascia.²⁸ Relatively little geometric analysis has been carried out on helixes in animal tissues but the helical geometry of plants is well recognized.
Flower heads display parallel spirals that run in opposite directions, a result of the most efficient packing arrangement of objects in their growing tips.^40,44 The number of elements within each opposing spiral is frequently two consecutive numbers of the Fibonacci sequence, where each new term is the sum of the two preceding ones (0,1,1,2,3,5,8,13,21,34…). The ratio of any two consecutive numbers approximates to the Golden Mean (0.61804), becomes closer as the sequence gets higher, and often appears in the proportions of biological structures.⁴⁵ The pattern on the side of a pineapple and cactus relate to the same sequence^40,44 with the left- and right-handed helixes having different angles (fig. 1d). Similar descriptions of the Fibonacci sequence in animal tissues are less common, with the only substantive examples in humans being the arrangement of microtubular components within the cell,⁴⁶ the position of coronary artery lesions⁴⁷ and packing arrangement of tropocollagen molecules within collagen fibrils.⁴⁸ However, keratin scales on the limbs of the [mammalian] pangolin (manis spp.) also bear a close resemblance to this pattern (fig. 2) while those on the body are similar to the alignment in figure 1c.

If the mean alignments of left- and right-handed collagen helixes in human limb fascia differ in a similar way to the Pangolin, an increase in the volume of myofascial tubes, due to cyclic fluctuations in vascular volume,^20,24 could lead to corresponding changes in rotation, length and width³⁶ that are palpable as helical motion (fig. 1d).

DISCUSSION

The left- and right-handed collagen fibre angles in bovines (~55^o)^30,31 were recorded from samples taken near the midline (Sternomandibularis m.) and it may be inevitable that they are the same (fig. 1c),^33,??,41 because both sides of the mammalian body wall are subject to the same influences during development.⁴⁹ Although fibre angles in the human thoraco-lumbar fasciae are quoted as the mean angle between crossed-fibre orientations, rather than individually, they are presumed to be similar on both sides.³² Fibre angles in the crural fascia are described in the same way,³² but as the developing limb is subject to eccentric influences^50,51 it might produce crossed-helical angles within the myofascia that are not the same but mirror each other on either side of the body.

Geometric patterns such as the helix do not just appear out of nowhere but because of the interactions between some basic physical principles,³⁹ and those that relate to the Fibonacci Sequence naturally result from the sequential growth of a self-organizing process under geometric constraint, ie a developing tube.^37,38,48 Although the Pangolin is the only mammal with this outward characteristic, this pattern may be an intrinsic part of mammalian limb development, and its appearance in myofascial tissues may have been overlooked simply because it was not anticipated.

Helical fibre arrays allow pressurized tubes to bend smoothly without kinking and resist torsional deformation,⁵² and the functional value of such movements in the elephant’s trunk, octopus tentacles and mammalian tongue are attributed to variable asymmetries in the helical angles of muscles and associated fascia.⁵³ As bone, muscle and fascia are all derived from the same embryonic mesenchyme and are thus specializations of the same tissue, it is likely that differences in crossed-helical fibre angles would become embedded within them all; and the movement of synovial joints around helical-like axes⁵⁴ may be due to this arrangement in surrounding tissues.

The effect of treatment

It is assumed that the difference in helical angles in the ‘ideal normal’ limb would be similar throughout (fig. 1d) and vary proportionately according to changes in fascial tension during joint movement.^32,35 However, changes in tension along any particular myofascial sheath due to posture, trauma or pathology would also alter the alignment of collagen helixes and conceivably change the pattern of motion palpable at the surface. The relative amounts of expansion, rotation and length change are then likely to vary between individuals because all myofascial tubes will be contributing to a unique 3-dimensional tension pattern.

Collagen fibres have a wavy crimped appearance that offers little resistance to stretch until straightened out under tension (<5%)⁴¹ and the transfer of tension through the myofascia (as the CRI) would probably be below this limit. Although proteoglycans play a crucial role in linking collagen fibres together,³¹ actively contracting myofibroblasts may be involved in maintaining particular configurations in response to normal and abnormal tensile stresses.^55,56 Angelsky et al (2005)⁵⁷ observed pre-clinical destructive changes in the polarization properties and fractal character of fascial tissues with degenerative-dystrophic pathologies, and future research might correlate this with palpatory findings.

The precise method of treatment is beyond the scope of this paper but anecdotally is reported to influence such conditions as ‘tennis elbow’, ‘repetitive strain injury’, lymphoedoema and phlebitis. It may be that the normalization of aberrant stresses in fascial tissues has an influence on cell function through the PRM.

The Primary Respiratory Mechanism

The value of the ‘PRM’ to normal physiology is not yet established but remains at the centre of the ‘cranial’ approach to treatment. It has always been assumed that Sutherland’s ‘five phenomena’ are directly associated with the driving force behind fascial motion in the rest of the body, but it may be that Traube-Hering-Mayer oscillations in the vascular system also provide a path for the CRI to reach the limbs, as described above.

The fascial network is continuous with the extracellular matrix (ECM) surrounding virtually every cell in the body, and both are part of the PRM;¹ the ECM also connects and transfers tension through transmembrane proteins to an internal cellular lattice called the cytoskeleton. Changes in cytoskeletal tension cause enzymes and substrates situated on the lattice to alter their activity, influencing cellular respiration and metabolism, and ultimately switching between different functional states such as growth, differentiation or apoptosis.⁵⁸ Ingber (2008)⁵⁸ and Levin (1995)⁵⁹ described the fascia/ECM/cytoskeleton as a single pre-tensioned tensegrity configuration, where a force applied to one part is distributed throughout the entire system, although the details of this are incomplete. As oscillations are a common feature in human physiology,²² a cyclic transfer of tension into the cytoskeleton may also enhance cellular metabolism, and be amenable to therapeutic intervention through the cranial and fascial parts of the PRM.

CONCLUSION

Cyclic changes in vascular fluid volume correspond with a similar expansion in limb volume²⁴ and may be palpable at the surface as the CRI. An increase in the volume of myofascial ‘tubes’ will increase the tension in collagen fibres and cause them to react according to the mechanics of crossed-helixes;^{33,34,37,38,53} the tubes then expand and change in length in a way that depends on the fibre angle (fig. 1a-c). A difference in fibre angle between left- and right-handed helixes in the limbs (fig. 1d) may also cause a rotation,³⁶ with helical motion that is palpable, and this conjecture is supported by a comparison of helixes in humans and other species (fig. 2).^40,44-48,53

If normal function relates to this geometric alignment of collagen, then ‘aberrant’ tensile stresses due to posture, trauma and pathology could alter the normal tension pattern and change fascial mechanics,⁶⁰ leading to the anomalies observed on palpation and the symptoms of such vague conditions as repetitive strain injury (RSI) and tennis elbow; treatment might then reverse this process and return the tissues to normal.

Further examination of the histology and mechanics of myofascial tissues is needed to confirm the proposed mechanism, and treatment methods require clinical trials; this approach to treatment might then become more widely accepted in the amelioration of certain limb pathologies.

REFERENCES

1. Parsons J and Marcer N. Osteopathy, Models for diagnosis, treatment and practice. Elsevier Churchill Livingstone. 2006; pp.201-18.

2. Sergueef N. Cranial osteopathy for infants, children and adolescents. Churchill Livingston Elsevier. 2007; p68 & 107.

3. McGrath MC. Viewpoint to: Ferguson A. A review of the physiology of cranial osteopathy. J Osteo Med 2003; 6:85-6.

4. Hartman SE. Should osteopathic licensing examinations test for knowledge of cranial osteopathy? Letter to the Editor. Int J Osteo Med 2005;8:153-4.

5. Jordan T. Swedenborg’s influence on Sutherland’s ‘Primary Respiratory Mechanism’ model in cranial osteopathy. Int J Osteo Med 2009;12:100-5.

6. Sutherland WG. The cranial bowl. Free Press Company. 1939.

7. Nelson K. Low frequency oscillations in human physiology and cranial osteopathy. Am Acad Osteo J 2011;21:12-23.

8. Woods JM, Woods RH. A physical finding relating to psychiatric disorders. J Am Osteo Assoc 1961;60:988-93.

9. Chaitow L. Cranial manipulation theory and practice. Churchill Livingstone. 1999.

10. Ferguson A. A review of the physiology of cranial osteopathy. J Osteo Med 2003; 6:74-88.

11. Magoun HI, (Ed). Osteopathy in the cranial field. The Cranial Academy. 1976.

12. Upledger JE, Vredevoogd JD. Craniosacral therapy. Eastland Press. 1983.

13. Moskalenko UE, Kravchenko TI, Vainshtein GB, Halvorson P, Feilding A, Mandara A, et al. Slow-wave oscillations in the craniosacral space: a hemoliquorodynamic concept of origination Neurosci Behav Physiol 2009;39:377-81.

14. Moss ML. The pathogenesis of premature cranial synostosis in man. Acta Anat 1959;37:351–70.

15. Richtsmeier JT, Aldridge K, Deleon VB, Panchal J, Kane AK, Marsh JL, et al. Phenotypic integration of neurocranium and brain. J Exp Zool 2006;306B:360–78.

16. Sabini RC, Elkowitz DE. Significance of differences in patency among cranial sutures. J Am Osteo Assoc 2006;106:600–4.

17. Cotton F, Rozzi FR, Valee B, Pachai C, Hermier M, Guihard-Costa AM, et al. Cranial sutures and craniometric points detected on MRI. Surg Radiol Anat 2005;27:64–70.

18. Mao JJ. Calvarial development: cells and mechanics. Curr Opin Orthop 2005;16:331-7.

19. Scarr G. A model of the cranial vault as a tensegrity structure, and its significance to normal and abnormal cranial development. Int J Osteo Med 2008;11:80-9.

20. Nelson KE, Sergueef N, Lipinski CM, Chapman AR, Glonek T. Cranial rhythmic impulse related to the Traube-Hering-Mayer oscillation: comparing laser-Doppler flowmetry and palpation. J Am Osteo Assoc 2001;101:163-73.

21. Green C, Martin CW, Bassett K, Kazanjian A. A systematic review of craniosacral therapy: biological plausibility, assessment reliability and clinical effectiveness. Compl Ther Med 1999;7:201-7.

22. Sircar S. Principles of medical physiology. Georg Thieme Verlag. 2008.

23. Moskalenko YE, Frymann V, Weinstein GB, Semernya VN, Kravchenko TI, Markovets SP et al. Slow rhythmic oscillations within the human cranium: phenomenology, origin and informational significance. Human Physiol 2001;27:171-8.

24. Christ F, Raithel P, Gartside IB, Gamble J, Peter K, Messmer K. Investigating the origin of cyclic changes in limb volume using mercury-in-silastic strain gauge plethysmography in man. J Physiol 1995;487:259-72.

25. Nelson KE, Sergueef N, Glonek T. Recording the rate of the cranial rhythmic impulse. J Am Osteo Assoc 2006;106:337-41.

26. Karni Z, Upledger JE, Mizrahi J, Heller L, Becker E, Najenson T. Examination of the cranial rhythm in long-standing coma and chronic neurologic cases. In: Upledger JE, Vredevoogd JD. Appendix B, Craniosacral therapy; Eastland Press. 1983.

27. Guimberteau JC, Setucq-Rigall J, Panconi B, Boileau R, Mouton P, Bakhach J. Introduction to the knowledge of subcutaneous sliding system in humans. Annales de Chirurgie Plastique Esthetique 2005;50:19-34.

28. Stecco L. Fascial Manipulation for Musculoskeletal Pain. Piccin Nuova Libraria; Padova. 2004.

29. Stecco A, Macchi V, Stecco C, Porzionato A, Day JA, Delmas V, et al. Anatomical study of myofascial continuity in the anterior region of the upper limb. J Bodyw Mov Thera 2009;13:53-62.

30. Purslow PP. The morphology and mechanical properties of endomysium in series-fibred muscles: variations with muscle length. J Musc Res Cell Motil 1994;15:299-308.

31. Purslow PP. Muscle fascia and force transmission. J Bodyw Mov Thera 2010;14:411-7.

32. Benetazzo L, Bizzego A, De Caro R, Frigo G, Guidolin D, Stecco C. Surg Radiol Anat 2011;33:855-62.

33. Clark RB, Cowey JB. Factors controlling the change of shape of certain nemertean and turbellarian worms. J Exp Biol 1958;35:731-48.

34. Shadwick R. Foundations of animal hydraulics: geodesic fibres control the shape of soft bodied animals. J Exp Biol 2008;211:289-91.

35. Chaudhry H, Max R, Stecco A, Findley T. Mathematical model of fiber orientation in anisotropic fascia layers at large displacements. J Bodyw Mov Thera 2012;16:158-64.

<36. Scarr G. Unpublished.

37. Pickett GT, Gross M, Okuyama H. Spontaneous chirality in simple systems. Phys Rev Letts 2000;85:3652-5.

38. Nisoli C, Gabor NM, Lammert PE, Maynard JK, Crespi VH. Annealing a magnetic cactus into phyllotaxis. Phys Rev E 2010;81:046107.

39. Scarr G. Helical tensegrity as a structural mechanism in human anatomy. Int J Osteo Med 2011;14:24-32.

40. Rothen F, Koch AJ. Phyllotaxis, or the properties of spiral lattices. I. Shape invariance under compression. J Phys France 1989;50:633-57.

41. Pabst DA. To bend a dolphin: convergence of force transmission designs in cetaceans and scombrid fishes. Am Zool 2000;40:146-55.

42. Holzapfel GA. Collagen in arterial walls: biomechanical aspects. In: Fratzl P, Editor. Collagen: structure and mechanics. Springer; 2008: pp. 285-324.

43. Hukins DWL, Meakin JR. Relationship between structure and mechanical function of the tissues of the intervertebral joint. Am Zool 2000;40:42-52.

44. Douady S, Couder Y. Phyllotaxis as a physical self-organized growth process. Phys Rev Letts 1992;68:2098-101.

45. Bolliger B, Erbudak M, Hensch A. “Pentepistemology” of biological structures and quasicrystals, in: Moran-Lopez JL. Ed. Physics of low dimensional systems. Kluwer Academic/Plenum Publishers; New York. 2002.

46. Hameroff S, Tuszynski J. Quantum states in proteins and protein assemblies: the essence of life? Proc. SPIE Fluctuations and Noise in Biological, Biophysical, and Biomedical Systems II, Eds. Abbott D, Bezrukov SM, Der A, Sánchez A. 2004;5467:27–41.

47. Gibson CM, Gibson WJ, Murphy SA, Marble SJ, McCabe CH, Turakhia MP et al. Association of the Fibonacci cascade with the distribution of coronary artery lesions responsible for ST-segment elevation myocardial infarction. Am J Cardiol 2003;1:595-7.

48. Charvolin J, Sadoc JF. A phyllotactic approach to the structure of collagen fibrils. Biophys Rev Letts 2011;6:13-27.

49. Koob TJ, Long JH. The vertebrate body axis: evolution and mechanical function. Am Zool 2000;40:1-18.

50. Blechschmidt E. The ontogenetic basis of human anatomy: a biodynamic approach to development from conception to adulthood. Ed. Freeman B. North Atlantic Books. 2004.

51. Henderson JH, Carter DR. Mechanical induction in limb morphogenesis: the role of growth-generated strains and pressures. Bone 2002:31:645-53.

52. Etnier SA. Twisting and bending of biological beams: distribution of biological beams in a stiffness mechanospace. Biol Bull 2003;205:36-46.

53. Kier WM, Smith KK. Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrostats. Zool J Linn Soc 1985;83:307-24.

54. Standring S. Gray’s anatomy, 39th ed. Elsevier, Churchill Livingstone. 2005: p 111.

55. Langevin HM, Cornbrooks CJ, Taatjes DJ. Fibroblasts form a body-wide cellular network. Histochem Cell Biol 2004;122:7-15.

56. Schleip R, Naylor IL, Ursu D, Melzer W, Zorn A, Wilke HJ, et al. Passive muscle stiffness may be influenced by active contractility of intramuscular connective tissue. Med Hypoth 2006;66:66-71.

57. Angelsky OV, Tomka YY, Ushenko AG, Ushenko YG, Ushenko YA. Investigation of 2D Mueller matrix structure of biological tissues for pre-clinical diagnostics of their pathological states. J Phys D Appl Phys 2005;38:4227-35.

58. Ingber DE. Tensegrity-based mechanosensing from macro to micro. [Review] Biophys Mol Biol 2008;9:163-79.

59. Levin SM. The importance of soft tissues for structural support of the body. Spine: State of the Art Reviews 1995;9:357-63.

60. Scarr G. A consideration of the elbow as a tensegrity structure. Int J Osteo Med 2012;15:53-65.