Traube-Hering-Mayer Waves
FASCIAL HIERARCHIES AND THE RELEVANCE OF CROSSED-HELICAL ARRANGEMENTS OF COLLAGEN TO CHANGES IN SHAPE
PART II: THE PROPOSED EFFECT OF BLOOD PRESSURE (TRAUBE-HERING-MAYER) WAVES ON THE FASCIA.
Journal of Bodywork and Movement Therapies
2016;20:629-638 link
Graham Scarr
CBiol., FRSB., FLS., DO request copy
ABSTRACT
Periodic changes in arterial and volume have long been related to respiratory and sympathetic nerve activity (Traube-Hering-Mayer waves) but their origins and nomenclature have caused considerable confusion since they were first discovered in the eighteenth century. However, although they remain poorly understood and the underlying details of their control are complicated, these waves do provide valuable clinical information on the state of blood pressure regulation in both normal and pathological conditions; and a correlation with oscillatory motions observed by certain practitioners suggests that they may also have some physiological value that relates to changes in the volume of fascial ‘tubes’.
Part I of this paper (Scarr, 2016) described a complex fascial network of collagen-reinforced tubular sheaths that are an integral part of muscle structure and function, and continuous with ‘higher-level’ fascial tubes surrounding groups of muscles, the limbs and entire body. The anisotropic arrangements of collagen fibres within the walls of these tubes reflect the most efficient distribution of mechanical stresses and have been considered to coordinate changes in shape, and a proposed link between cyclic variations in arterial pressure and volume, and the behaviour of these fascial compartments is now described.
KEYWORDS
Arterial pressure waveform; Collagen; Cranial rhythmic impulse; Fascia; Helix; Interstitial fluid flow; Mayer waves; Myofascia; Traube Hering.
INTRODUCTION
The fascia
 Once dismissed as a packing tissue of little consequence, the fascia is now recognized as a continuous and interconnected structural network that permeates and envelops almost every part of the body, and it has many diverse and important functional roles (Schleip et al 2012; Tozzi 2015a,b). Scarr (2016) described the hierarchical structure of muscles as a complex network of collagen-reinforced tubular sheaths, which enclose the myofibres and are continuous with ‘higher-level’ fascial tubes (compartments) surrounding groups of muscles, the limbs and entire body (Benjamin 2009); and this description of fascial tissues as ‘tubes’ naturally follows from their cross-sectional appearances (figure 1).
Once dismissed as a packing tissue of little consequence, the fascia is now recognized as a continuous and interconnected structural network that permeates and envelops almost every part of the body, and it has many diverse and important functional roles (Schleip et al 2012; Tozzi 2015a,b). Scarr (2016) described the hierarchical structure of muscles as a complex network of collagen-reinforced tubular sheaths, which enclose the myofibres and are continuous with ‘higher-level’ fascial tubes (compartments) surrounding groups of muscles, the limbs and entire body (Benjamin 2009); and this description of fascial tissues as ‘tubes’ naturally follows from their cross-sectional appearances (figure 1).
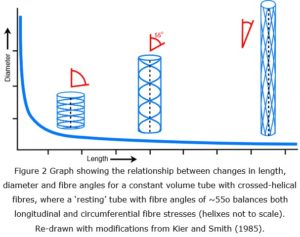
In 1958, Clarke and Cowey showed that changes in the relative length and diameter of nemertean and turbellarian worms were controlled by the particular alignment of tensioned fibres within their body walls, where the fibres were constrained by the crossed-helical geometry surrounding the pressurized body tube and enabled it to maintain a constant volume throughout changes in shape (figure 2); and this basic model has now become entrenched as a design principle in biomechanics (Wainwright 1988; Shadwick 2008; Kier 2012).
A crossed-helical tube that is shortened will cause the fibre angles to increase (relative to the tube axis) while one that is extended in length will cause them to decrease; and in both cases, the tension within the fibres becomes greater as the tube shape moves away from its central resting position (Purslow 1989; Goriely and Tabor 2013). The shape that optimally balances both longitudinal and circumferential stresses is when the fibres are at an angle of 54.44o, i.e. the fibre orientations are reflecting the most efficient distribution of mechanical stresses and coordinating the changes in shape of the tube, as well as providing a system of elastic energy storage that assists in returning the tube to its resting state (Clarke & Cowey 1958).
Although the functional significance of this particular arrangement is now well established in many species and in different parts of the body, it has received relatively little attention within the fascia of humans, and the theory and relevance of this pattern to changes in the shape of muscles was described in Scarr (2016). The formation of a crossed-helical pattern is based on simple geometric principles (Pickett et al 2000; Scarr 2011) and its persistence is ensured because it is one of the most stable of structural configurations; and it is not surprising that such a system should predominate in compliant biological tissues because this is one of the most efficient ways of optimizing the stresses within their walls (Clarke and Cowey 1958; Wainwright 1988; Kier 2012).
Anecdotally, certain practitioners routinely observe an oscillatory tissue motion that is palpable on the surface of the body and provides qualitative information that contributes to the diagnosis and treatment of a wide variety of conditions (Parsons and Marcer 2006 p 201-218; Sergueff et al 2011); and Scarr (2013) described a potential link with crossed-helical arrangements of collagen. Nelson et al (2001 & 2006) also found a correlation with cyclic changes in arterial blood flow and it is now proposed that all these factors relate to changes in the volume of tubular fascial sheaths.
Traube-Hering-Mayer waves
While periodic changes in arterial pressure and volume have long been recognized, their physiological origins and nomenclature have caused considerable confusion since they were first described in the eighteenth century (Koepchen 1984; Larsen et al 2010), but they do provide valuable clinical information through the real-time monitoring of haemodynamic parameters and contribute to the decision making process within intensive care units (Lamia et al 2005). They are also useful to research in understanding cardio-respiratory coupling (Larsen et al 2010; Dick et al 2014); central and baroreflex control (Julien 2006; Morris et al 2010); peripheral blood flow related to sympathetic nerve activity (SNA) (Barman 2009; Fatouleh and Macefield 2013) and changes in tissue volume and perfusion (Christ et al 1995) under normal and pathological conditions.
Part II now explains a mechanism whereby cyclic changes in arterial pressure and volume might influence the behaviour of the crossed-helical fascial compartments surrounding them; and briefly describes the physiological implications.
BLOOD PRESSURE WAVES
Blood pressure waves appear at various frequencies, recorded as cycles per minute (cpm) or cycles per second (Hz), and are classified into three main groups: a very-low frequency band (0.00 – 0.18 cpm, 0.00 – 0.03 Hz); low-frequency (Mayer) waves that are influenced by baroreflex activity (1.8 cpm – 9.0 cpm, 0.03 – 0.15 Hz); and a faster Traube-Hering wave band associated with the respiratory cycle (9.0 – 24.0 cpm, 0.15 – 0.4 Hz). Although each group has traditionally implied a different mechanism of causation, the precise boundaries between each one can vary because of experimental and inter-species differences, etc (Acharya et al 2005; Finucane et al 2010) and the differences between them are not clear cut.
Traube-Hering waves
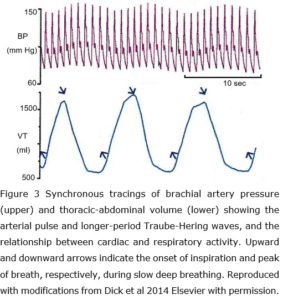 The appearance of Traube-Hering waves (9.0 – 24.0 cpm, 0.15 – 0.4 Hz) in the peripheral circulation is a reflection of respiratory sinus arrhythmia (RSA), a normal physiological phenomenon that reciprocally couples the respiratory rate with that of the heart, where inspiration and expiration cause momentary changes in heart rate and arterial pressure (figure 3), but the underlying details of their control are complex. Respiratory activity is normally monitored through mechanoreceptors (thorax) and chemoreceptors (blood gases), and this information is relayed to the brainstem and ultimately the heart through reflex changes in sympathetic and parasympathetic outflow, with cardiac activity then leading to changes in blood pressure and baroreflex stimulation that influence the respiratory centres through complex feedback loops (Larsen et al 2010; Ben-Tal et al 2012; Dick et al 2014).
The appearance of Traube-Hering waves (9.0 – 24.0 cpm, 0.15 – 0.4 Hz) in the peripheral circulation is a reflection of respiratory sinus arrhythmia (RSA), a normal physiological phenomenon that reciprocally couples the respiratory rate with that of the heart, where inspiration and expiration cause momentary changes in heart rate and arterial pressure (figure 3), but the underlying details of their control are complex. Respiratory activity is normally monitored through mechanoreceptors (thorax) and chemoreceptors (blood gases), and this information is relayed to the brainstem and ultimately the heart through reflex changes in sympathetic and parasympathetic outflow, with cardiac activity then leading to changes in blood pressure and baroreflex stimulation that influence the respiratory centres through complex feedback loops (Larsen et al 2010; Ben-Tal et al 2012; Dick et al 2014).
Mayer waves
The origins of Mayer waves, on the other hand, have been the subject of a great deal of speculation, and Julien (2006) reviewed and summarized some of the experimental findings. The pacemaker theory “…is based on the observation that… oscillations of sympathetic nerve activity (SNA) and/or hemodynamic variables can be observed at or near the frequency of Mayer waves in the absence of sensory inputs from the periphery. Such rhythmicity is then thought to derive from the pacemaker-like activity of an autonomous oscillator located within central nervous structures generating SNA” (Julien 2006). In other models, it was anticipated that “the numerous dynamic components and fixed time delays present in the baroreflex loop would result in the production of a resonant, self-sustained oscillation of arterial pressure” but Julien (2006) also suggested that “Mayer waves are transient oscillatory responses to hemodynamic perturbations rather than true feedback oscillations”.
Dick et al (2014) showed that respiratory activity can also be modulated with the arterial pulse in humans, and Morris et al (2010) detailed a coupling between the respiratory rhythm, vagal activity and Mayer wave-related oscillations in cats that involved “reciprocal parallel signalling paths between the pons and ventral respiratory column”. These later findings thus support the presence of a central Mayer-wave oscillator that is bi-directionally coupled with respiratory oscillators, but it “remains to be shown whether the raphe-pontine network is directly involved in production of the 0.1 Hz rhythm or receives an efference copy generated elsewhere” (Morris et al (2010).
The function of arterial pressure waves
The rather variable nature of these oscillations under different experimental conditions has led to suggestions that any perceived functions are purely incidental, particularly with Mayer-waves, although this has naturally been subject to speculation (Polosa 1984; Miyakawa 1984; Nelson et al 2001, 2006). Barman (2009) noted, with respect to peripheral SNA, that “these rhythms can be entrained to inputs such as baroreceptor and lung inflation afferents and central respiratory networks, which give rise to their characteristic rhythmic pattern”, and that “rhythmic activity may lead to more effective activation of sympathetic neurons than randomly occurring activity… and is important in coordinating activity in different sympathetic nerves, and… may help homeostasis”. Ben-Tal et al (2012) hypothesized that “RSA helps the heart do less work while maintaining healthy levels of blood gases” and Dick et al (2014) even considered that “cardio-respiratory coupling is a biomarker of health”!
Regardless of their perceived ‘functions’, arterial pressure waves are known to reflect the state of blood pressure regulation in both normal (Julien 2006; Fatouleh and Macefield 2013) and pathological conditions (Christ et al 1995; Heusser et al 2010; Finucane et al 2010); and a correlation with the ‘cranial rhythmic impulse’ (CRI) recognized by certain groups of practitioners suggests that they also have some physiological and therapeutic value that relates to changes in the volume of fascial tubes (Scarr 2013).
A CHANGE IN VOLUME
The fascial tube
Within muscles, the perimysium and epimysium frequently contain two crossed-ply sets of collagen ‘cables’ aligned at about ± 55o (relative to the long axis) (Rowe 1981; Passerieux et al 2007; Purslow 2010), while the apparently isotropic alignments of collagen fibres within the endomysium appear to be random but collectively have a (numbers-weighted) mean orientation of about 59o (Purslow and Trotter 1994). These collagen fibre angles increase with muscle contraction and become more aligned with its transverse or circumferential plane, and when the muscle is stretched the angles decrease as the fibres become aligned towards the main direction of tension, indicating that the collagen fibres are mechanically linked with each other (figure 2) (Purslow 1989; Purslow 2010; Chaudhry et al 2012).
The deep or investing fascia is a tougher tissue that surrounds and contains groups of muscles (compartments), and is continuous with aponeuroses (Mcombe et al 2001; Stecco and Stecco 2012a & b) and the overlying ‘superficial’ fascia that lies beneath the skin (Benjamin 2009; Abu-Hijleh et al 2012); and all are involved in the transfer of tension (Maas and Sandercock 2010; Huijing 2012), with the loose fibre network of the superficial layer contributing to its flexibility (Iatridis et al 2003). Although bundles of collagen fibres within the investing fascia have been found to be aligned at 0o (McCombe et al 2001; Benjamin 2009), Benetazzo et al (2011) noted the mean angle between crossed-fibre orientations in human thoraco-lumbar and crural fascia as 78o, which indicates an average fibre angle of 39o relative to the body axis.
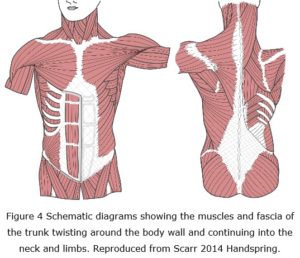 Hebrank (1980) showed that the dermis of eels (Anguillidae) contains crossed-helical arrangements of collagen fibres aligned at 45o, while Naresh et al (1997) observed angles (50o – 70o) that varied between different parts of the skin in sharks (Odontaspididae); and Pabst (2000) found a similar pattern within the body walls of tuna fish (Scombridae), dolphins and whales (Cetacea: Mammalia). Crossed-helical alignments of muscles and connective tissues also occur within the mammalian tongue, octopus tentacles and the elephant’s trunk etc (Kier and Smith 1985), which all suggests that similar patterns are likely to occur in humans (Scarr, 2016). Whilst these examples are structural specializations whose prime function is to facilitate movement and locomotion, the alignments of muscle and investing fascial tissues that curve around the body wall and limbs are also suggestive of helical arrangements, if only in part (figure 4) (Benetazzo et al 2011; Vleeming 2012).
Hebrank (1980) showed that the dermis of eels (Anguillidae) contains crossed-helical arrangements of collagen fibres aligned at 45o, while Naresh et al (1997) observed angles (50o – 70o) that varied between different parts of the skin in sharks (Odontaspididae); and Pabst (2000) found a similar pattern within the body walls of tuna fish (Scombridae), dolphins and whales (Cetacea: Mammalia). Crossed-helical alignments of muscles and connective tissues also occur within the mammalian tongue, octopus tentacles and the elephant’s trunk etc (Kier and Smith 1985), which all suggests that similar patterns are likely to occur in humans (Scarr, 2016). Whilst these examples are structural specializations whose prime function is to facilitate movement and locomotion, the alignments of muscle and investing fascial tissues that curve around the body wall and limbs are also suggestive of helical arrangements, if only in part (figure 4) (Benetazzo et al 2011; Vleeming 2012).
Scarr (2016) concluded that these crossed-helical arrangements of collagen within muscles and ‘higher-level’ fascial sheaths are likely to be contributing to their dynamic behaviour, which introduces another factor into soft-tissue mechanics as these fascial tubes contain blood vessels that are continuously changing in volume.
Arteries and the fascia
 Arterial walls provide reinforcement against the pressure of blood and regulate its flow by contracting and dilating under autonomic nervous system control (vasomotion), with a cyclic increase in circumference and volume (dilation) corresponding with a decrease in pressure, and vice versa (Sircar 2008 p 302); and it should be no surprise that the collagen fibres within their walls are also arranged in crossed-helical arrangements (Holzapfel 2006). Regular oscillations of arterial pressure and volume (Traube-Hering-Mayer waves) are then likely to influence the behaviour of the tissues surrounding them, and indeed, Christ et al (1995) found a correspondence between cyclic increases in arterial volume and changes in the volume of the limb (< 0.177 ml per 100 ml tissue).
Arterial walls provide reinforcement against the pressure of blood and regulate its flow by contracting and dilating under autonomic nervous system control (vasomotion), with a cyclic increase in circumference and volume (dilation) corresponding with a decrease in pressure, and vice versa (Sircar 2008 p 302); and it should be no surprise that the collagen fibres within their walls are also arranged in crossed-helical arrangements (Holzapfel 2006). Regular oscillations of arterial pressure and volume (Traube-Hering-Mayer waves) are then likely to influence the behaviour of the tissues surrounding them, and indeed, Christ et al (1995) found a correspondence between cyclic increases in arterial volume and changes in the volume of the limb (< 0.177 ml per 100 ml tissue).
Muscles are essentially incompressible (Baskin and Paolini 1966) and there are no empty spaces in surrounding tissues that could absorb these changes in volume, which means that a cyclic dilation and contraction of these fascial tubes in sympathy with changes in vascular volume (both intra- and extra-muscular) might be able to influence the crossed-helical fibre configurations within their walls in a particular way.
Figure 5 a-c shows how an increase in arterial volume might cause a surrounding fascial tube with a low collagen fibre angle to increase more in diameter, one with a high angle to increase more in length, and one with an angle of 54.44o to balance both tendencies; with even longitudinally oriented fibres (0o) that occur in some epimysial and deep fascial tissues (McCombe et al 2001; Benjamin 2009) leading to an expansion in tube width.
DISCUSSION
A change in volume
While direct measurements of periodic changes in arterial blood pressure (Lamia et al 2005; Dick et al 2014) (figure 3) and flow (laser-Doppler flowmetry) are widely used, the electrical recording of sympathetic nerve activity (Barman 2009; Fatouleh and Macefield 2013) and plethysmographic volume changes also provide information on local tissue physiology (Gamble et al 1993; Christ et al 1995; Joyner et al 2001). Plethysmography demonstrates the changes in volume that occur within an organ or limb through the direct displacement of water, or variations in its circumference (mercury-in-silastic strain gauge MSG), which is particularly relevant here because of the potential influence that cyclic changes in arterial volume have on crossed-helical fascial tubes (figure 5).
Christ et al 1995 recorded (MSG) periodic volume changes of < 0.177 ml per 100 ml of tissue in the lower limb of patients under positive-pressure ventilation at 9.0 – 19.5 cpm (0.15 – 0.325 Hz), whilst this author observed cyclic volume changes < 0.20 ml in the whole forearm in three subjects during spontaneous breathing (water-displacement plethysmograph based on the design by Raine and Sneddon 2002); and all appeared to correlate with the Traube-Hering wave frequencies given earlier. In this author’s investigation, oscillating volume changes of less than 0.01 ml (10 µl) matched the frequency of the radial pulse, but as no continuous recording was available any slower Mayer-wave-like patterns could not be recognized. Christ et al (1995), however, recorded low-frequency volume changes between 0.5 and 7.0 cpm (0.008 – 0.117 Hz) and attributed them to variations in arteriolar vasoconstriction (and possibly venous and lymphatic vessels), but excluded “Traube-Hering-Brauer” (sic) waves as a possible cause because they were “nearly always observed unilaterally”; but the underlying pathologies of the subjects may have influenced this finding and suggests that this conclusion might have been premature.
A note on modelling
It should be noted that the apparently continuous fibers that stretch between the ends of the crossed-helical tubes (figures 2 and 5) are really graphic representations of bundles of smaller collagen molecules/fibrils that are cross-linked together and transfer tensional forces between them (Avery and Bailey 2008). These bundles are frequently wavy, or crimped, with a crimp angle of ~ 39o that enables them to be elastically stretched by an additional five per cent of their length; and this angle decreases as the fibres are straightened out (and tension increases) during changes in tube length and circumference. Purslow (1989) found a correlation between crossed-helical fibre angles and changes in sarcomere length, where fibre angles of 20o and 80o in the perimysium corresponded with sudden and dramatic increases in stiffness (from 0 to ~18 KPa) and set a boundary limit to further changes in shape, which also supports the predictions made by Clarke and Cowey (1958) for elastic fibre systems. While muscles normally operate well within the central region between these two extremes and are thus able to change shape with ease, information on the fibre angles and behaviour of the surrounding deep/investing fasciae are less well described.
It should be emphasized that there is considerable variation in the shape and cross-sectional area of all these fascial sheaths/tubes, and that the connections and interactions between them within the overall structural hierarchy are highly complex and not completely characterized (Scarr, 2016); and the model described here merely serves as an illustration of the crossed-helical principles that may contribute to the mechanical behaviour of all these fascial tubes.
The cranial rhythmic impulse (CRI)
Anecdotally, ‘cranial osteopaths’ and ‘cranio-sacral therapists’ routinely observe an oscillatory tissue motion that is palpable on the surface of the body and provides qualitative information that contributes to the diagnosis and treatment of a wide variety of conditions (Parsons and Marcer 2006 pp 201-218; Sergueff 2007). Nelson et al (2001) compared different CRI frequencies with blood velocity measurements taken on the ear lobe (laser-Doppler flowmetry), where Fourier transform and power-spectral analysis revealed distinct peaks that matched the ‘very low-frequency’, ‘Mayer’ and ‘Traube-Hering’ wave groups described above; although their naming of them was not consistent with these. Nelson et al (2006) found that the mean palpated rate of the CRI fell within the Mayer group but then related them to Traube-Hering oscillations in a 1:2 relationship, while Nelson (2011) dispensed with these names altogether.
This frequency-domain type of analysis is widely used to isolate particular wave frequencies but can lead to misleading results on its own and does not necessarily provide useful information on the cause or regulation of these waves. The Poincaré plot would thus be valuable in future studies because it also reveals the relationship between consecutive wave cycles and conveniently summarizes all the information (Acharya et al 2005; Dick et al 2014). Scarr (2013) briefly reviewed some of the experimental evidence concerning the relationship between oscillations in blood flow and the CRI, and found that although a statistical correlation between them could be made, there was considerable confusion surrounding all these enigmatic waves.
A different pattern
Scarr (2013) also noted that the CRI and certain palpatory phenomena observed in the limbs might be explained by a different crossed-helical arrangement within the fascia, where a subtle sense of the limb shortening, expanding in width and rotating externally is followed by a lengthening, narrowing and internal rotation (Nelson et al 2006; Sergueef 2007 p 68); or in other words, a slowly oscillating (Mayer wave-like frequency), low amplitude helical torsioning of the entire limb. While a shortening/expansion and lengthening/narrowing oscillation resulting from changes in volume would certainly be compatible with the crossed-helical mechanics shown in figure 5a-c, the rotational component remains outside of this model; but a preliminary experiment showed that a crossed-helical tube with the left- and right-handed fibres oriented at different angles caused a shortening and torsional strain when the tube volume was increased (figure 5d) (see Appendix).
 Whilst this experiment is very simplistic when compared with the complex structural reality of the fascia, both Wainwright (1988 p 71) and Kier (2012) depict drawings of crossed-helical tubes with fibres of different angles (although they give no examples or explanation for this particular pattern), and Goriely and Tabor’s (2013) analysis of the physics underlying such an arrangement in a biological context adds support to the feasibility of this model. Scarr (2013) also suggested that a similar pattern of scales on the limbs of the pangolin (Manis spp) might reflect this alignment within the underlying fascial sheaths, and be an “intrinsic part of mammalian limb development”, but this remains a conjecture (figure 6). Even so, geometric patterns do not just appear out of nowhere but because of the interactions between some basic physical principles and the constraints that underlie all self-organizing processes; and crossed-helical arrangements are a natural consequence of these (Pickett et al 2000; Snir and Kamien 2005; Scarr 2011, 2014).
Whilst this experiment is very simplistic when compared with the complex structural reality of the fascia, both Wainwright (1988 p 71) and Kier (2012) depict drawings of crossed-helical tubes with fibres of different angles (although they give no examples or explanation for this particular pattern), and Goriely and Tabor’s (2013) analysis of the physics underlying such an arrangement in a biological context adds support to the feasibility of this model. Scarr (2013) also suggested that a similar pattern of scales on the limbs of the pangolin (Manis spp) might reflect this alignment within the underlying fascial sheaths, and be an “intrinsic part of mammalian limb development”, but this remains a conjecture (figure 6). Even so, geometric patterns do not just appear out of nowhere but because of the interactions between some basic physical principles and the constraints that underlie all self-organizing processes; and crossed-helical arrangements are a natural consequence of these (Pickett et al 2000; Snir and Kamien 2005; Scarr 2011, 2014).
The tensioned tissue pump
The vascular tree
It has so far been proposed that cyclic variations in blood volume/pressure within the arteries and arterioles (Traube-Hering-Mayer waves), which are the result of rhythmic variations in sympathetic nerve activity on vessel calibre (Barman 2009; Fatouleh and Macefield 2013), are the driving force behind changes in the volume of the fascial tubes surrounding them; and the relevance of this model is most clear in the limbs, which consist of tubular fascial compartments containing bones, muscles, blood vessels and nerves that are generally oriented along the main limb axis. Larger arteries run within the deep investing fascia (figure 1b) and send one or more branches that travel within the connective tissue framework of each muscle, with smaller arteries and arterioles running parallel and ramifying in the perimysial septa before giving off capillaries that anastomose within the endomysium (Standring 2005 p118). While propagation of the arterial pulse (systolic/diastolic pressure 120/80 mm Hg) is extremely complicated and depends in part on the distensibility of different regions of the vascular tree, mean blood pressure is considerably reduced in the arterioles (>18 mm Hg; Sircar 2008 p251); and the pulse greatly damped by the time it reaches the capillary bed (Ethier and Simmons 2007 p179).
Although the measurement of intra-muscular pressures is notoriously difficult (Hill 1948; Hargens et al 1989; Ward et al 2007), Nakhostine et al (1993) showed that the pressure within human anterior tibialis increases centripetally (~26 mm Hg compared to ~4 mm Hg near the muscle surface), while an extensive review by Aweid et al (2012) found that the generally accepted normal pressure of 6 – 12 mm Hg at rest could rise to 141 mm Hg during activity; and should be considered pathological if it remains above 34 mm Hg after one minute following exercise (compartment syndrome). The ability of any particular vessel to initiate changes in the volume of the fascial tube(s) surrounding it may thus depend on the local pressure differentials between them; and influence their contents.
The interstitium
The exchange of fluids within the extra-cellular matrix (ECM)/interstitial tissues is driven by the flow of plasma through the walls of blood capillaries, and its removal through the venous and lymphatic system, and it may also be that slowly oscillating changes in the volume of tubular fascial compartments are able to create a pumping action that increases the flow of fluids within them (Rutkowski & Swartz 2006; Meert 2012). While the local interchange of fluids is essential to the supply and removal of substances associated with cell metabolism and is greatly enhanced by muscle contraction (Sircar 2008 p 231), a continuous low-frequency pump would ensure that this is maintained at rest; and the principle of this has already been outlined by certain practitioners as the CRI and ‘primary respiratory mechanism’ (Nelson et al 2001; Parsons and Marcer 2006 p 204; Scarr 2013).
Higher-level’ fascial tubes are really structural continuations of the ECM/interstitial tissues that surround myofibres and virtually every other cell in the body, with the intimate connections between them and the cellular cytoskeleton, such as transmembrane proteins (Brown et al 2012) and perimysial junction plates (Passerieux et al 2006), enabling the transfer of tensional forces in both directions and influencing cell function in complex ways (Scarr, 2016). Changes in cytoskeletal tension, coupled with chemical signalling, cause the enzymes and substrates situated on this lattice to alter their metabolic activities and influence cellular respiration, as well as switching between different functional states such as growth, differentiation or apoptosis (Wang et al, 2009; Ingber et al 2014).
In short, it may be that changes in fascial tension caused by cyclic variations in volume (in response to blood pressure waves) are transferrable to the ECM and cytoskeleton and thereby alter cellular activity. Oscillating changes in cytoskeletal tension and fluid flow as the result of this vascular driven fascial mechanism might then have an effect on the normal maintenance, remodelling and development of all tissues throughout the body (Nelson et al 2005; Ingber et al 2014).
CONCLUSION
The myofascia is a fibrous specialization of fascial/ECM tissues that enclose and inter-penetrate muscles as a complex hierarchy of tubes containing smaller tubes within them; and is continuous with higher-level fascial tubes that surround groups of muscles, the limbs and entire body (figure 1). Bundles of collagen fibres within the perimysium and epimysium are typically aligned in two distinct directions that together form crossed-helical patterns (figure 2), and this arrangement also appears within the deep investing fascia surrounding groups of muscles and the body wall.
Scarr (2016) described how this particular geometric configuration might coordinate changes in muscle shape (length versus circumference) during contraction and extension, with collagen fibre tension increasing towards both these extremes and settling at an intermediate resting angle of ~55o (relative to the tube axis), and the orientation of the fibres varying between a high-angle on shortening and a low-angle when elongated (figure 2). In essence, the particular fibre orientations are a reflection of the most efficient distribution of mechanical stresses; and the same basic principles are likely to apply to the walls of all these tubular sheaths (Appendix).
It has thus been proposed that cyclic variations in arterial pressure and volume (figure 3) (Traube-Hering-Mayer waves) are likely to cause corresponding changes in the volume and shape of the tubular fascial compartments surrounding them (figure 5); and that the effects of this may be palpable on the surface of the body as the CRI. If this really is the case, then such rhythmic changes in volume would probably have an effect on the flow of fluids within the ECM/interstitium, with variations in tissue tension also influencing the behaviour of associated cells; and such oscillations may even play a role in the development and regulation of particular tissue shapes and patterns throughout life.
APPENDIX
An experiment to show that an increase in the volume of a crossed-helical tube with differing fibre angles causes a torsional strain.
 This demonstration is the previously unpublished ‘preliminary experiment’ referred to by Scarr (2013 ref 36) and omitted from that paper because the value of such a simple and apparently unique experiment was not fully appreciated at the time. It is essentially a qualitative assessment of the changes that occur following an increase in volume of a crossed-helical tube made from two sets of stretchable cords or ‘fibres’ with differing orientations (figure 7).
This demonstration is the previously unpublished ‘preliminary experiment’ referred to by Scarr (2013 ref 36) and omitted from that paper because the value of such a simple and apparently unique experiment was not fully appreciated at the time. It is essentially a qualitative assessment of the changes that occur following an increase in volume of a crossed-helical tube made from two sets of stretchable cords or ‘fibres’ with differing orientations (figure 7).
Apparatus:
- Two circular plywood plates (thickness 3 mm, diameter 100 mm) were drilled with twelve holes (2.5 mm) spaced around a circle (80 mm diameter) in preparation for the cord attachments, with similar holes drilled in the centre of each plate to allow for final stabilization of the apparatus, and a single hole (16 mm diam.) in the top plate to permit insertion of a balloon. The top plate was then screwed and fixed into position on the supporting stand.
- A continuous length of 1.0 mm polyester cord (‘Shamballa jade’ as used in bead jewellery) was woven between each end plate using consecutive holes and forming a tube with a length of about 200 mm. The tension in each cord (fibre) was then equalized by rotating the lower end-plate and gently pulling down several times before securing those parts of the cords (lying on the outer face of the plywood) with a drop of superglue (cyanoacrylate).
- A second length of cord was then inserted through one of the same holes of the upper plate and interwoven in a clockwise direction between five of the above cords (starting on the outside of the adjacent cord) and passed through the sixth hole of the lower plate. It was then interwoven back to the top plate, parallel with the previous cord, and the process repeated until each hole contained two ‘fibres’.
- With the wall of this crossed-helical tube now in place, the lengths of this second set of ‘fibres’ were now equalized and secured (as described in (1) above) so as to form a set with a distinctively higher angle (relative to the tube axis) compared to the first set. The tube had a final length of 190 mm with end diameters of 80 mm, a set of left-handed helixes at 10o, and another set of right-handed helixes at 22o.
- Finally, a plastic protractor for measuring axial rotation was screwed onto the underside of the lower end-plate; a fixed point marker secured to the stand; and the end of a piece of string secured in the central hole in the lower plate, with the other end attached to a small mass that just removed any slack from the helical ‘fibres’.
Method:
The initial protractor angle was noted and a long rubber balloon (rather than a pear shape) was inserted through the large hole in the fixed upper end-plate and attached to a plastic hand pump. The balloon was inflated so that it pushed against all the crossed-helical tube ‘fibres’ and simulated an increase in tube volume; and finally tied at its end after removing the pump. The new protractor angle and length between the end-plates were then noted so as to assess the changes that followed balloon inflation.
Results:
The lower end-plate was found to have rotated in a clockwise direction (viewed from below) with a change in angle from 111o to 127o, relative to the fixed upper plate, and a reduction in length between the plates from 190 mm to 180 mm. The length of the tube had thus shortened by 10 mm and the ends had twisted by 16o in relation to each other, as a result of the balloon inflation, and these changes followed the orientation of the highest fibre-angle (right-handed helix) as shown in figure 5d. Although the particular cord used could be stretched to almost 10% of its length, which is about twice the amount that crimped collagen fibres can be elongated to (Purslow 1989), it is still consistent with the fibre model described by Clarke and Cowey (1958).
Conclusion:
This ‘preliminary experiment’ showed that an increase in volume of a crossed-helical tube constructed from left- and right-handed fibres with different angles causes a torsion that follows the orientation of the highest fibre-angle; and is consistent with the theoretical analysis of Goriely and Tabor (2013). Although the fibre angles of 10o and 22o were appreciably different from those described in the body of the text, and such an arrangement of collagen fibres within the fascia of the limbs remains speculation, it provided a qualitative demonstration of the principle and now requires more detailed analysis of fascial histology.
ACKNOWLEDGEMENTS
I would like to thank Emma Colley for information on the clinical value of arterial pressure waves; Stephen Dibnah and Leonid Blyum for their participation in the author’s plethysmography experiment; and to the anonymous reviewer who rigorously questioned the assumptions made and provided much-needed food for thought.
REFERENCES
Abu-Hijleh M, Dharap AS, Harris PF 2012 Fascia superficialis. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh 19-23.
Acharya R, Kannathal N, Hua LM, Yi LM 2005 Study of heart rate variability signals at sitting and lying postures. Journal of Bodywork and Movement Therapies 9: 134-141.
Avery NC, Bailey AJ 2008 Restraining cross-links responsible for the mechanical properties of collagen fibers: natural and artificial. In: Fratzl P (ed) Collagen: structure and mechanics. Springer, New York; 81-110.
Aweid O, Del Buono A, Malliaras P, Iqbal H, Morrissey D, Maffulli N, Padhiar N 2012 Systematic review and recommendations for intracompartmental pressure monitoring in diagnosing chronic exertional compartment syndrome of the leg. Clinical Journal of Sports Medicine 22: 356-370.
Barman SM 2009 Sympathetic nerve activity has more character than you may think. Journal of Physiology 587.20: 4767-4768.
Baskin RJ, Paolini PJ 1966 Muscle volume changes. Journal of General Physiology 49: 387-404.
Benetazzo L, Bizzego A, De Caro R, Frigo G, Guidolin D, Stecco C 2011 3D reconstruction of the crural and thoracolumbar fasciae. Surgical and Radiologic Anatomy 33: 855-862.
Benjamin M 2009 The fascia of the limbs and back – a review. Journal of Anatomy 214: 1-18.
Ben-Tal A, Shamailov SS, Paton JFR 2012 Evaluating the physiological significance of respiratory sinus arrhythmia: looking beyond ventilation-perfusion efficiency. Journal of Physiology 590.8: 1989-2008.
Brown SC, Mueller U, Conti FJ 2012 Integrins in the development and pathology of skeletal muscle. In: Zaher A (ed) Neuromuscular disorders InTech 1-20.
Chaudhry H, Max R, Stecco A, Findley T 2012 Mathematical model of fiber orientation in anisotropic fascia layers at large displacements. Journal of Bodywork and Movement Therapies 16: 158-164.
Christ F, Raithel P, Gartside IB, Gamble J, Peter K, Messmer K 1995 Investigating the origin of cyclic changes in limb volume using mercury-in-silastic strain gauge plethysmography in man. Journal of Physiology 487: 259-272.
Clark RB, Cowey JB 1958 Factors controlling the change of shape of certain nemertean and turbellarian worms. Journal of Experimental Biology 35: 731-748.
Dick TE, Mims JR, Hsieh YH, Morris KF, Wehrwein EA. 2014 Increased cardio-respiratory coupling evoked by slow deep breathing can persist in normal humans. Respiratory Physiology and Neurobiology 204: 99-111.
Ethier CR, Simmons CA 2007 Introductory mechanics: from cells to organisms. Cambridge University Press, Cambridge.
Fatouleh R, Macefield VG 2013 Cardiorespiratory coupling of sympathetic outflow in humans: a comparison of respiratory and cardiac modulation of sympathetic nerve activity to skin and muscle. Experimental Physiology 98.9: 1327-1336.
Finucane C, Boyle G, Fan CW, Hade D, Byrne L, Kenny RA 2010 Mayer wave activity in vasodepressor carotid sinus hypersensitivity. Eurospace 12: 247-253.
Gamble J, Gartside IB, Christ F 1993 A reassessment of mercury in silastic strain gauge plethysmography for microvascular permeability assessment in man. Journal of Physiology 464: 407-422.
Goriely A, Tabor M 2013 Rotation, inversion and perversion in anisotropic elastic cylindrical tubes and membranes. Proceedings of the Royal Society A 469:20130011.
Hargens AR, Akeson WH, Mubarak SJ, Owen CA, Gershuni DH, Garfin SR, Lieber RL, Danzig LA, Botte MJ, Gelberman RH 1989 Tissue fluid pressures: from basic research tools to clinical applications.
Hebrank MR 1980 Mechanical properties and locomotor functions of eel skin. Biological Bulletin 158: 58-68.
Heusser K, Tank J, Engeli S, Diedrich A, Menne J, Eckert S, Peters T, Sweep FCGJ, Haller H, Pichlmaier AM, Luft FC, Jordan J 2010 Carotid baroreceptor stimulation, sympathetic activity, baroreflex function and blood pressure in hypertensive patients. Hypertension 55: 619-626.
Hill AV 1948 The pressure developed in muscle during contraction. Journal of Physiology 107: 518-526.
Holzapfel GA 2006 Determination of material models for arterial walls from uniaxial extension tests and histological structure. Journal of Theoretical Biology 238: 290-302.
Huijing PA 2012 Myofascial force transmission. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. Fascia: the tensional network of the human body. Elsevier Edinburgh pp 117-122.
Iatridis JC, Wu J, Yandow JA, Langevin HM 2003 Subcutaneous tissue mechanical behaviour is linear and viscoelastic under uniaxial tension. Connective Tissue Research 44: 208-217.
Ingber DE, Wang N, Stamenovic D 2014 Tensegrity, cellular biophysics and the mechanics of living systems. Reports on Progress in Physics 77: 046603.
Joyner MJ, Dietz NM, Shepherd JT 2001 From Belfast to Mayo and beyond: the use and future of plethysmography to study blood flow in human limbs. Journal of Applied Physiology 91: 2431-2441.
Julien C 2006 The enigma of Mayer waves: facts and models. Cardiovascular Research 70: 12-21.
Kier WM, Smith KK 1985 Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrostats. Zoological Journal of the Linnean Society 83: 307-324.
Kier WM 2012 The diversity of hydrostatic skeletons. Journal of Experimental Biology 215: 1247-1257.>
Koepchen HP 1984 History of studies and concepts of blood pressure waves. In: Miyakawa K, Koepchen HP, Polosa C eds. Mechanisms of blood pressure waves. Japan Scientific Societies Press and Springer-Verlag, Tokyo 3-23.
Lamia B, Chemla D, Richard C, Teboul JL 2005 Clinical review: interpretation of arterial pressure waves in shock states. Critical Care 9: 601-606.
Larsen PD, Tzeng YC, Sin PYW, Galletly DC 2010 Respiratory sinus arrhythmia in conscious humans during spontaneous respiration Respiratory Physiology and Neurobiology 174: 111-118.
Maas H, Sandercock TG 2010 Force transmission between synergistic skeletal muscles through connective tissue linkages. Journal of Biomedicine and Biotechnology 575672 doi:10.1155/2010/575672.
McCombe D, Brown T, Slavin J, Morrison WA 2001 The histochemical structure of the deep fascia and its structural response to surgery. Journal of Hand Surgery (British and European Volume 26B: 89-97.
Meert GF 2012 Fluid dynamics in fascial tissues. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh 177-181.
Miyakawa K 1984 Blood pressure waves as an adaptation. In: Miyakawa K, Koepchen HP, Polosa C eds. Mechanisms of blood pressure waves. Japan Scientific Societies Press and Springer-Verlag, Tokyo 119-135.
Morris KF, Nuding SC, Segers LS, Baekey DM, Shannon R, Lindsey BG, Dick TE 2010 Respiratory and Mayer wave-related discharge patterns of raphé and pontine neurons change with vagotomy Journal of Applied Physiology 109: 189-202.>
Nakhostine M, Styf JR, Van Leuven S, Hargens AR, Gershuni DH 1993 Intramuscular pressure varies with depth: the tibialis anterior muscle studied in 12 volunteers. Acta Orthopaedica Scandinavica 64: 377-381.
Naresh MD, Arumugam V, Sanjeevi R 1997 Mechanical behaviour of shark skin. Journal of Bioscience 22: 431-437.
Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS 2005 Emergent patterns of growth controlled by multicellular form and mechanics. Proceedings of the National Academy of Science 102: 11594-11599.
Nelson KE, Sergueef N, Lipinski CM, Chapman AR, Glonek T 2001 Cranial rhythmic impulse related to the Traube-Hering-Mayer oscillation: comparing laser-Doppler flowmetry and palpation. Journal of the American Osteopathic Association 101; 163-173.
Nelson K, Sergueef N, Glonek T 2006 Recording the rate of the cranial rhythmic impulse. Journal of the American Osteopathic Association 106: 337-341.
Nelson K 2011 The 2010 Northup memorial lecture: low frequency oscillations in human physiology and cranial osteopathy. The American Academy of Osteopathy Journal 21: 12-23.
Pabst DA 2000 To bend a dolphin: convergence of force transmission designs in Cetaceans and Scombrid fishes. American Zoologist 40: 146-155.
Parsons J, Marcer N 2006 Osteopathy: models for diagnosis, treatment and practice. Elsevier Edinburgh.
Passerieux E, Rossignol R, Chopard A, Carnino A, Marini JF, Letellier T, Delage JP 2006 Structural organization of the perimysium in bovine skeletal muscle: junctional plates and associated intracellular subdomains. Journal of Structural Biology 154: 206-216.
Passerieux E, Rossignol R, Letellier T, Delage JP 2007 Physical continuity of the perimysium from myofibers to tendons: involvement in lateral force transmission in skeletal muscle. Journal of Structural Biology 159: 19-28.
Pickett GT, Gross M, Okuyama H 2000 Spontaneous chirality in simple systems. Physical Review Letters 85: 3652-3655.
Polosa C 1984 Rhythms in the activity of the autonomic nervous system: their role in the generation of systemic arterial pressure waves. In: Miyakawa K, Koepchen HP, Polosa C eds. Mechanisms of blood pressure waves. Japan Scientific Societies Press and Springer-Verlag, Tokyo 27-41.
Purslow PP 1989 Strain-induced reorientation of an intramuscular connective tissue network: implications for passive muscle elasticity. Journal of Biomechanics 22: 21-31.
Purslow PP 2010 Muscle fascia and force transmission. Journal of Bodywork and Movement Therapies 14: 411-417.
Purslow PP, Trotter JA 1994 The morphology and mechanical properties of endomysium in series-fibred muscles: variations with muscle length. Journal of Muscle Research and Cell Motility 15: 299-308.
Raine NM, Sneddon JC 2002 A simple water-filled plethysmograph for measurement of limb blood flow in humans. Advances in Physiology Education 26: 120-128.
Rowe RWD 1981 Morphology of perimysial and endomysial connective tissue in skeletal muscle. 13: 681-690.
Rutkowski JM, Swartz MA 2007 A driving force for change: interstitial flow as a morphoregulator. Trends in Cell Biology 17: 44-50.
Scarr G 2011 Helical tensegrity as a structural mechanism in human anatomy. International Journal of Osteopathic Medicine 14: 24-32.
Scarr G 2013 Palpatory phenomena in the limbs: a proposed mechanism. International Journal of Osteopathic Medicine 16: 114-120.
Scarr G 2014 Biotensegrity: the structural basis of life. Handspring, Edinburgh.
Scarr G 2016 Fascial hierarchies and the relevance of crossed-helical arrangements of collagen to changes in the shape of muscles. Journal of Bodywork and Movement Therapies.
Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh.
Sergueef N 2007 Cranial osteopathy for infants, children and adolescents. Churchill Livingstone Elsevier Edinburgh.
Sergueef N, Greer MA, Nelson KE, Glonek T 2011 The palpated cranial rhythmic impulse (CRI): its normative rate and examiner experience. International Journal of Osteopathic Medicine 14: 10-16.
Shadwick RE 2008 Foundations of animal hydraulics: geodesic fibres control the shape of soft bodied animals. Journal of Experimental Biology 211: 289-291.
Sircar S 2008 Principles of medical physiology. Thieme Stuttgart.
Snir Y, Kamien RD 2005 Entropically driven helix formation Science 307: 1067.
Standring S 2005 Gray’s anatomy 39th ed. Elsevier Churchill Livingstone, Edinburgh.
Stecco C, Stecco A 2012 Deep fascia of the shoulder and arm. Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 25-29.
Stecco C, Stecco A 2012 Deep fascia of the lower limbs. Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 31-35.
Tozzi P 2015a A unifying neuro-fasciagenic model of somatic dysfunction – underlying mechanisms and treatment – Part I. Journal of Bodywork and Movement Therapies 19: 310-326.
Tozzi P 2015b A unifying neuro-fasciagenic model of somatic dysfunction – underlying mechanisms and treatment – Part II. Journal of Bodywork and Movement Therapies 19: 526-543.
Vleeming A 2012 The thoracolumbar fascia: an integrated functional view of the anatomy of the TLF and coupled structures. In: Schleip R, Findley TW, Chaitow L, Huijing PA eds. 2012 Fascia: the tensional network of the human body. Elsevier, Edinburgh pp 37-43.
Wainwright SA 1988 Axis and circumference: the cylindrical shape of plants and animals. Harvard University Press, Cambridge.
Wang N, Tytell JD, Ingber DE 2009 Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nature Reviews 10: 75-82.
Ward S, Davis J, Kaufman KR, Lieber RL 2007 Relationship between muscle stress and intramuscular pressure during dynamic muscle contractions. Muscle Nerve 36: 313-319.
