Helix
HELICAL TENSEGRITY AS A STRUCTURAL MECHANISM IN HUMAN ANATOMY
International Journal of Osteopathic Medicine
2011;14:24-32. link
Graham Scarr request copy
ABSTRACT
Tensegrity is a structural system popularly recognized for its distinct compression elements that appear to float within a tensioned network. It is an attractive proposition in living organisms because such structures maintain their energy-efficient configuration even during changes in shape. Previous research has detailed the cellular cytoskeleton in terms of tensegrity, being a semi-autonomous system amenable to such analysis because of its size. It has also been described at higher levels in the extracellular/fascial matrix and musculo-skeletal system, but there are fewer syntheses of this.
At a fundamental level, the helix and tensegrity share common origins in the geometries of the platonic solids, with inherent hierarchical potential that is typical of biological structures. The helix provides an energy-efficient solution to close-packing in molecular biology, a common motif in protein construction, and a readily observable pattern at many size levels throughout the body. The helix and tensegrity are described in a variety of anatomical structures, suggesting their importance to structural biology and manual therapy.
INTRODUCTION
The world of biology is full of weird and wonderful shapes, some with no obvious purpose, and others that suggest some hidden meaning. Even human anatomy has its fair share of the bizarre in the shapes of bones and limbs. How and why does each one develop its characteristic form, and how does that relate to function? Is there more to shape than genetics and Wolffs’ Law?
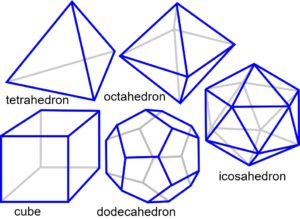 Three thousand years ago, the Greeks believed that just five archetypal forms could describe everything in the universe, because they were pure and perfect, and part of natural law. Recent research reinstates these physical laws as a major determinant of biological complexity in the sub-cellular realms, and significant to structures at higher scales.1-4
Three thousand years ago, the Greeks believed that just five archetypal forms could describe everything in the universe, because they were pure and perfect, and part of natural law. Recent research reinstates these physical laws as a major determinant of biological complexity in the sub-cellular realms, and significant to structures at higher scales.1-4
Tensegrity (tension-integrity) is a structural mechanism that potentially integrates anatomy from the molecular level to the entire body, and is popularly recognized for its distinct compression elements that appear to float within a tensioned network. It is a most attractive proposition in living systems, because such structures automatically assume a position of stable equilibrium, with a configuration that minimizes their stored elastic energy. Tensegrity structures allow movement, with the minimum of energy expenditure, without losing stiffness or stability.1,5-7
This contrasts with the orthodox view that explains the musculo-skeletal system through classical Newtonian mechanics, using pillars, arches and fixed-fulcrum levers to counteract the force of gravity. In this approach, bones stack on top of one another like a pile of bricks, restrained by soft tissues that permit movement in a local piece-meal like way.8 Comparisons of tensegrity and biological structures show them both to have non-linear visco-elastic properties, with fluid-like movements that result from integration of all components in the system.1,5,6,9
The molecular helix provides an energy-efficient solution to close-packing in biology and also displays tensegrity properties. It is a common motif in protein construction, and a readily observable pattern at many size levels throughout the body. It is proposed that helical tensegrity is a key mechanism in structural biology and consequently has significance for manual therapies.
THE HELIX
 The helix is like a coiled spring, or put mathematically, “A spiral curve lying on a cone or cylinder, and cutting the generators at a constant angle” (Walker, 1991).10,11 In biology, it can be appreciated as a regular stacking of discrete components, such as the nucleotides and bases in DNA, or the steps in a spiral staircase.
The helix is like a coiled spring, or put mathematically, “A spiral curve lying on a cone or cylinder, and cutting the generators at a constant angle” (Walker, 1991).10,11 In biology, it can be appreciated as a regular stacking of discrete components, such as the nucleotides and bases in DNA, or the steps in a spiral staircase.
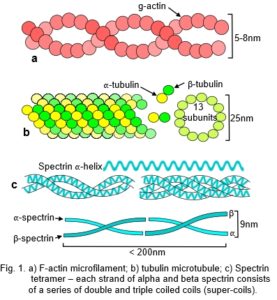
Globular proteins, often containing multiple helical domains, can themselves polymerize into helixes (fig. 1a,b).12 Similar helixes can wind around each other to form coiled-coils (Fig. 1c),13 and assemble into mechanically rigid rods or filaments, or further combine into more complex structures with specialized functions (fig. 2).
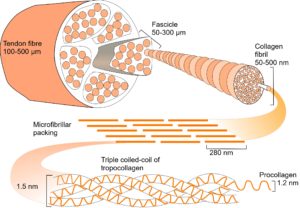
In collagen type I, repeating sequences of amino acids spontaneously form a left-handed helix of procollagen, with three of these helixes combining to form a right-handed helix of tropocollagen. Five tropocollagen molecules then coil in a staggered helical array,14 which lengthens longitudinally by the addition of more tropocollagen to form a microfibril, with higher arrangements forming fibrils, fibres and fascicles.15 Collagen appears at several different hierarchical levels within bones, tendons, ligaments and fascia (fig. 2).
Structural hierarchies
 Hierarchies link structures at multiple levels and are widespread in living organisms. They provide an efficient mechanism for packing in 3-D16 by using components that are made from smaller components, with each made from smaller still, often repeating in a fractal-like manner (fig. 2).1,5,17 Hierarchies enable mechanical forces to be transferred down to a smaller scale with the dissipation of potentially damaging stresses.18-21At atomic and molecular levels, the basic forces of attraction and repulsion automatically balance those stresses in the most energetically efficient configuration.12,22-24
Hierarchies link structures at multiple levels and are widespread in living organisms. They provide an efficient mechanism for packing in 3-D16 by using components that are made from smaller components, with each made from smaller still, often repeating in a fractal-like manner (fig. 2).1,5,17 Hierarchies enable mechanical forces to be transferred down to a smaller scale with the dissipation of potentially damaging stresses.18-21At atomic and molecular levels, the basic forces of attraction and repulsion automatically balance those stresses in the most energetically efficient configuration.12,22-24
Helical tubes
The tubular nature of the helix scales up into blood vessels,25 the urinary system and intestinal tract.26,27 Carey (1920) observed left and right-handed helical patterns in the epithelium during formation of the oesophagus and trachea, respectively, in the early embryo.28 In the walls of elastic arteries, such as the aorta, helical collagen reinforcement resists high loads from the pressure of blood. The middle layer organizes into lamellar units, with the orientation of collagen fibres and smooth muscle cells forming a continuous helix. Collagen is more dispersed in the outer adventitia, but still forms two helical groups of fibres.25
Within the spine, the intervertebral disc contains collagen arranged in concentric lamellae, with opposing orientations in alternate helical layers of 65o (axial).29 The inner lamellae of the annulus fibrosus consist of collagen type II fibres, cross-linked to type IX on the fibre surface, within a highly hydrated proteoglycan matrix; gradually changing to collagen type I fibres in the outer lamellae.30,31 The higher proteoglycan/water content in the inner lamellae acts as a thick-walled pressure vessel containing the nucleus pulposus, while the higher concentration of collagen type I in the outer lamellae provides tensile reinforcement during bending and torsion.29,32
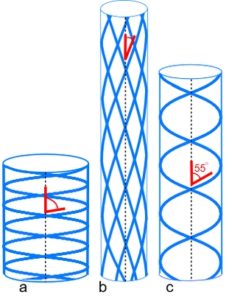 Pressurized tubes cause circumferential and longitudinal stresses in the tube wall that are typically contained by collagen under tension within a helix. Clarke and Cowey (1958) showed that an optimum fibre angle of ~55o (axial) balances both these stresses, with a reduced angle resisting tube elongation, and a higher angle resisting circumferential and volume increases.33,34 Such helical fibre arrays allow pressurized tubes to bend smoothly without kinking, and resist torsional deformation;32 collagen has itself been described as a tube.35
Pressurized tubes cause circumferential and longitudinal stresses in the tube wall that are typically contained by collagen under tension within a helix. Clarke and Cowey (1958) showed that an optimum fibre angle of ~55o (axial) balances both these stresses, with a reduced angle resisting tube elongation, and a higher angle resisting circumferential and volume increases.33,34 Such helical fibre arrays allow pressurized tubes to bend smoothly without kinking, and resist torsional deformation;32 collagen has itself been described as a tube.35
Cardiac muscle fibre orientation varies linearly between inner and outer walls, from 55o (axial) in one direction to 55o in the opposite, with tangential spiralling in a transverse plane.36 The entire heart has also been described as a helical coil of muscle with contractions that cause clockwise and anti-clockwise twisting motions.37 This typically produces a left ventricular ejection fraction of 60%, for a muscular contraction of just 15%,38 confirming the mechanical efficiency of a helix.
2.3 Tubes within tubes
Traditionally considered as mere packing tissue, fascia has been shown to exert considerable influence over muscle generated force transmission.39-42 It naturally develops into compartments, or ‘tubes within tubes’, particularly noticeable in cross-sections of the limbs. Within muscle, a delicate network of endomysium surrounds individual muscle fibres and is continuous with the perimysium ensheathing groups of fibres in parallel bundles, or fasciculi. Perimysial septa are themselves inward extensions of the epimysium that covers the muscle and is continuous with the fascia investing whole muscle groups. All these sheaths (tubes) coalesce and transmit the force generated within muscle fibres through tendons and inter/extra-muscular fascial attachments.39,42 These fascial tissues are all reinforced by two helical crossed-ply sets of collagen,36 with the ‘ideal’ resting fibre orientation of 55o (axial)33 that varies with changing muscle length.
 Tubular organs that maintain constant volume throughout changes in shape, due to crossed-helical arrangements of muscle and fascial tissue, have been described in the tongues of mammals and lizards, the arms and tentacles of cephalopods, and the trunks of elephants.43 Helical winding and its functional significance have also been described in the body walls of worms;33 squid;44 amphibians;45 eels;46 fish and dolphins;47 suggesting that a similar helical arrangement is likely to occur throughout the human. However, although the thoraco-lumbar and abdominal muscle/fasciae appear to be partial spirals, information on the fibre orientation of other fascial compartments is incomplete.
Tubular organs that maintain constant volume throughout changes in shape, due to crossed-helical arrangements of muscle and fascial tissue, have been described in the tongues of mammals and lizards, the arms and tentacles of cephalopods, and the trunks of elephants.43 Helical winding and its functional significance have also been described in the body walls of worms;33 squid;44 amphibians;45 eels;46 fish and dolphins;47 suggesting that a similar helical arrangement is likely to occur throughout the human. However, although the thoraco-lumbar and abdominal muscle/fasciae appear to be partial spirals, information on the fibre orientation of other fascial compartments is incomplete.
 Stecco (2004) described helical fascial sheaths that transfer tensional forces within and between themselves, and control movement in a way that the nervous system is incapable of.48 Anecdotally, palpatory phenomena with a helical component are observed within the soft tissues of the extremities.49 A normal pattern exhibits right-handed helical motion in the limbs on the left side, and left-handed helical motion on the right, although current anatomical knowledge is unable to explain this.
Stecco (2004) described helical fascial sheaths that transfer tensional forces within and between themselves, and control movement in a way that the nervous system is incapable of.48 Anecdotally, palpatory phenomena with a helical component are observed within the soft tissues of the extremities.49 A normal pattern exhibits right-handed helical motion in the limbs on the left side, and left-handed helical motion on the right, although current anatomical knowledge is unable to explain this.
The helix has long been recognized in joint motion,8 and its widespread appearance at multiple size-scales throughout the body suggests that it has some special significance. At a fundamental level, the helix and tensegrity are linked through a common origin in the geometries of the platonic solids.1,4,50
SIMPLE GEOMETRY
The platonic solids, geodesic geometry and close-packing
 The platonic solids are regular polyhedra distinguished by having faces that are all the same shape, and naturally form through the efficiencies of geodesic geometry (the connection of points over the shortest path) and principles of symmetry.1,4,50 In two-dimensions, objects of similar size close-pack and form stable triangular configurations (fig. 3a). Adding another sphere to each triangle creates a tetrahedron, and the addition of more spheres allows the octahedron and cube to emerge (fig. 3b-c), because of the same packing arrangement. These platonic shapes are generally only found as fixed inorganic crystals, but there are many consequences of close-packing.
The platonic solids are regular polyhedra distinguished by having faces that are all the same shape, and naturally form through the efficiencies of geodesic geometry (the connection of points over the shortest path) and principles of symmetry.1,4,50 In two-dimensions, objects of similar size close-pack and form stable triangular configurations (fig. 3a). Adding another sphere to each triangle creates a tetrahedron, and the addition of more spheres allows the octahedron and cube to emerge (fig. 3b-c), because of the same packing arrangement. These platonic shapes are generally only found as fixed inorganic crystals, but there are many consequences of close-packing.
The icosahedron differs from the other platonic shapes by packing spheres around a nuclear space to form the geodesic dome (Fig. 3d).50 It is also triangulated and has multiple symmetries which allow it to stack in a column or helix and form more complex patterns and shapes.1,2 Some naturally occurring structures based on the icosahedron are carbon fullerenes; pollen grains and ‘spherical’ viruses.22-24
Both the tetrahedron and icosahedron spontaneously form through the interactions of natural physical forces, and are the basis for appreciating complex shapes in human anatomy.2,4,51
Chirality and Equivalence
The property of chirality is intrinsic to the helix, and the platonic solids demonstrate this as they polymerize into left and right-handed helixes (fig. 4).51-54 At a basic level, four spheres close-pack to form a tetrahedron, the shape that occupies the smallest proportion of unit space; minimum volume within maximum surface area.50 The addition of more spheres as in the lattice packing of figures 3b & 3c, alters that proportion because of the squares within the octahedron, but a tetrahelix comes closer to the optimum, making it a more suitable model for molecular packing because of this margin of energy-efficiency (fig. 4a).51,53,54 A tetrahelix also displays inherent hierarchy within its sub-helixes of different pitch (fig. 5).

 Mapping a tetrahelix onto a plane surface, by ‘unzipping’ one of its long helical edges, displays the packing efficiency of a triangular pattern (fig. 3a). Rolling that map into a cylinder demonstrates equivalence, where each component is in the same relative position to all the others.53,54 Equi-valence implies that components are arranged symmetrically, and the only shapes that can accommodate it have surfaces based on the platonic solids and cylinders.22-24,55,56 Because molecules in a peptide sequence are unlikely to match the points on a geometric lattice precisely, evolution has evaded this constraint through the device of ‘quasi-equivalence’, where component proteins contort slightly but still relate to the geometric template.1,23,24,53
Mapping a tetrahelix onto a plane surface, by ‘unzipping’ one of its long helical edges, displays the packing efficiency of a triangular pattern (fig. 3a). Rolling that map into a cylinder demonstrates equivalence, where each component is in the same relative position to all the others.53,54 Equi-valence implies that components are arranged symmetrically, and the only shapes that can accommodate it have surfaces based on the platonic solids and cylinders.22-24,55,56 Because molecules in a peptide sequence are unlikely to match the points on a geometric lattice precisely, evolution has evaded this constraint through the device of ‘quasi-equivalence’, where component proteins contort slightly but still relate to the geometric template.1,23,24,53
Tropocollagen (fig. 2) has been described as three stretched quasi-tetrahelixes surrounding a central core.53,54 Each glycine residue, from the three procollagen peptides, contributes a hydrogen atom that forms the corner of a regular tetrahedron, and together they form the right-handed tetrahelical core of the tropocollagen molecule. The left-handed procollagens are the sub-helixes shown in figure 5b; and this configuration also gives rise to a stack of slightly contorted icosahedra.53,54 Most (if not all) molecular helixes are geometrically related to the tetrahelix and icosahedron,12,22,53,54,56 including the alpha-helix of DNA, which has been described as a [triple stranded] tetrahelix with one strand missing.53
Molecules automatically assume a state of minimal-energy as they balance the attraction and repulsion of their constituent atoms. As the helix is a more efficient close-packing configuration it is understandable that it should be such a common structural shape. At a larger scale, the bacterial cell wall contains actin homologues arranged as a structural helix determining cell shape and elongation.57,58 Plants display similar configurations in their cell walls59 and geometric patterns at a higher level.
Fibonacci and the Golden Mean
 The number
The number ![]() of elements within each opposing spiral is nearly always two consecutive numbers of the Fibonacci sequence, where each new term is the sum of the two preceding ones (1,1,2,3,5,8,13,21,34…). The ratio of any two consecutive numbers approximates to the Golden Mean (1.61804), and becomes closer as the sequence gets higher. The helical pattern on the side of a pineapple, arrangement of branches on a plant stem61 and position of coronary artery lesions62 relate to the same sequence. The Golden Mean often appears in the proportions of biological structures and platonic solids,63 including the icosahedron, which is the model that takes us into the tensegrity of macro-anatomy.50
of elements within each opposing spiral is nearly always two consecutive numbers of the Fibonacci sequence, where each new term is the sum of the two preceding ones (1,1,2,3,5,8,13,21,34…). The ratio of any two consecutive numbers approximates to the Golden Mean (1.61804), and becomes closer as the sequence gets higher. The helical pattern on the side of a pineapple, arrangement of branches on a plant stem61 and position of coronary artery lesions62 relate to the same sequence. The Golden Mean often appears in the proportions of biological structures and platonic solids,63 including the icosahedron, which is the model that takes us into the tensegrity of macro-anatomy.50
TENSEGRITY
Descriptions of tensegrity in biology have appeared in the literature since the early 1980’s,64,65 and include the cellular cytoskeleton;5 developing neurites66 and cerebral cortex;67 spider silk6,68 and wasp arcus;69 mammalian70-72 and avian lung;73 fascial matrix;74-76 shoulder;75 spine;51 pelvis77 and cranium.78
Fuller (1975) described a tensegrity structure as a set of struts under compression, and an arrangement of cables under isometric tension, that always balances in the most energetically efficient configuration.50 It is geodesic by its very nature, because tension always acts in straight lines, and automatically reduces itself to a minimum. Tensegrity structures make possible an infinite variety of stable shapes through changes in the lengths of their compression members, and changes in those shapes that require very little control energy. As each component influences all the others, stresses distribute throughout the system, creating a structure that can react to external forces from any direction without collapsing.6,7,51 An organism utilizing such a system would be able to move with the minimum of energy expenditure without losing stiffness or stability.6,7,51 Because tension and compressional forces are separated, the material properties of components can be optimized, and in biological systems this typically occurs through hierarchies. Tensegrity hierarchies achieve a significant reduction in mass,6,7 and provide a functional connection at every level, from the simplest to the most complex, with the entire system acting as a unit.5,51,76
4.1 The tensegrity helix
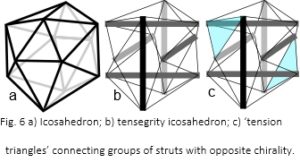 The icosahedron is a fundamental geometric shape because it encloses a greater volume, within minimum surface area, than any regular structure apart from a sphere (fig. 6a). It is developed into a tensegrity structure by using six compression struts to traverse the inside (fig. 6b). These connect and hold opposite vertices apart with the outer edges of the icosahedron now replaced by cables under tension. The resultant pull of the cables is balanced by the struts, which remain distinct from each other and do not touch. They provide structural integrity so that the compression elements float within the tension network.50,79
The icosahedron is a fundamental geometric shape because it encloses a greater volume, within minimum surface area, than any regular structure apart from a sphere (fig. 6a). It is developed into a tensegrity structure by using six compression struts to traverse the inside (fig. 6b). These connect and hold opposite vertices apart with the outer edges of the icosahedron now replaced by cables under tension. The resultant pull of the cables is balanced by the struts, which remain distinct from each other and do not touch. They provide structural integrity so that the compression elements float within the tension network.50,79
Considering the six struts in different groups of three, joined on the surface by ‘tension triangles’ (fig. 6c), shows that each strut within the group is oriented at 90o to the others, and together they create a chiral twist. On the other side of the structure is a similar group with a twist in the opposite direction, which means that a tensegrity icosahedron already contains helical precursors of both chiralities.
 When three struts are modelled on their own (Fig.7), they form a shape called a tensegrity prism.6,7 Increasing the number of struts causes their centres to position more towards the outside of the structure, enlarging the central space and eventually forming a cylindrical ‘wall’ due to the changing orientation (fig. 7b-d). The struts are equivalent, and all form part of an infinite series of left or right-handed helixes; the model in figure 8 demonstrates their tubular nature. Each strut could be made from a smaller helix, or the whole structure become part of a strut within a larger helix ie it has hierarchical capability. Helical molecules are at the ‘lower’ end of structural hierarchies that fill the entire body, but have physical properties that continue into those higher levels. Helical tensegrity is a structural mechanism with many properties useful to organic life.
When three struts are modelled on their own (Fig.7), they form a shape called a tensegrity prism.6,7 Increasing the number of struts causes their centres to position more towards the outside of the structure, enlarging the central space and eventually forming a cylindrical ‘wall’ due to the changing orientation (fig. 7b-d). The struts are equivalent, and all form part of an infinite series of left or right-handed helixes; the model in figure 8 demonstrates their tubular nature. Each strut could be made from a smaller helix, or the whole structure become part of a strut within a larger helix ie it has hierarchical capability. Helical molecules are at the ‘lower’ end of structural hierarchies that fill the entire body, but have physical properties that continue into those higher levels. Helical tensegrity is a structural mechanism with many properties useful to organic life.
THE HELICAL-TENSEGRITY BODY
Helical molecules behave as tensegrity structures in their own right, as they stabilize through a balance between the forces of attraction (tension) and repulsion (compression).79,80They readily combine into more complex structures that retain some of the same properties.2,12
 The cellular cytoskeleton is described as a multi-functional tensegrity structure that influences cell shape, and activates multiple intra-cellular signalling pathways.5 Helical microfilaments of actin and microtubules of tubulin are the tension and compression elements, respectively (fig. 1a,b); while spectrin fibres and actin bundles may have similar roles within the cell cortex (Figs. 1c).81,82Tensioned intermediate filaments link everything together, from the nucleus to the cell membrane.83
The cellular cytoskeleton is described as a multi-functional tensegrity structure that influences cell shape, and activates multiple intra-cellular signalling pathways.5 Helical microfilaments of actin and microtubules of tubulin are the tension and compression elements, respectively (fig. 1a,b); while spectrin fibres and actin bundles may have similar roles within the cell cortex (Figs. 1c).81,82Tensioned intermediate filaments link everything together, from the nucleus to the cell membrane.83
Tension is generated through the action of actomyosin motors and polymerization of microtubules, and any change in force at one part of the structure causes the cytoskeleton to alter overall cell shape.5 Many enzymes and substrates are situated on the cytoskeletal lattice, and changes in its configuration alter their activity, leading to a switch between different functional states such as growth, differentiation or apoptosis.5
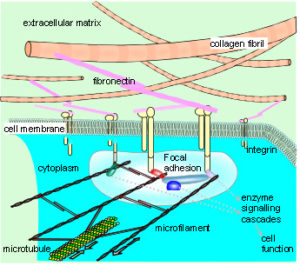 The cytoskeleton connects to the matrix and other cells through transmembrane proteins, such as integrins and cadherins, respectively. These create a mechanical coupling that transfers tension, generated within the cytoskeleton, to the matrix and adjacent cells. A prestressed state of isometric tension thus exists between them, so that a change in matrix tension causes a realignment of structures within the cytoplasm, and a change in cell function. This reciprocal transfer of mechanical forces is likely to orchestrate cellular growth and expansion, allowing the emergence of complex multi-cellular tissue patterns, based on the same principles.5,84,85
The cytoskeleton connects to the matrix and other cells through transmembrane proteins, such as integrins and cadherins, respectively. These create a mechanical coupling that transfers tension, generated within the cytoskeleton, to the matrix and adjacent cells. A prestressed state of isometric tension thus exists between them, so that a change in matrix tension causes a realignment of structures within the cytoplasm, and a change in cell function. This reciprocal transfer of mechanical forces is likely to orchestrate cellular growth and expansion, allowing the emergence of complex multi-cellular tissue patterns, based on the same principles.5,84,85
Helical tubes
The formation of capillaries results from tension-dependent interactions between endothelial cells and an extra-cellular scaffold of their own construction, and is described through tensegrity.86 The growing matrix causes changes in the configuration of cytoskeletal components,5 and initiates chemical signalling cascades that influence further development of the capillary network.87
The capacity for fluid flow through a tube depends, in part, on the porosity of the tube wall. The helical tensegrity ‘wall’ in figure 8 has many gaps, but if the struts were expanded into plates that just touched each other, they could be made to ‘seal’ the internal space. This compares with the selective barrier of endothelial cells that allows vascular contents to pass out between capillary walls. The internal cellular cytoskeleton determines cell shape and orientation, through tensegrity;5 is affected by signalling mechanisms and variations in fluid flow; and alters the tension between cells through adherens junctions,88 ultimately affecting tube permeability.89,90
In tensegrity terms, there is no specific need for a compressional element within the tube wall if this is provided by outward pushing radial pressure, although arterial walls are pre-stressed even when load free. It is likely that wall components under tension are linked to other structures under compression at different hierarchical levels; Fuller (1975) emphasized that tension and compression must always coexist.50 Collagen type I fibrils are the predominant tensors, and are virtually inextensible under tension (<5%);30 but the mechanical properties of more than twenty other types are poorly understood. Proteoglycans and glycosaminoglycans tend to increase in tissues under compression. Combining these and other components into tissue specific matrices contributes to huge histological variation. Confirmation that they are tensegrity configurations, however, will depend on analysis of their physical interactions.
A fundamental principle of tensegrity is that the forces of tension and compression are separated into different components, and always act in straight lines; which means that there are no shear stresses or bending moments. The model in figure 8 shows curved struts that seem contrary to this, but they can be understood in terms of hierarchies. Curved struts only remain stable if their crystal/molecular structures are strong enough to resist the potentially damaging shear stresses that lead to buckling; or they are part of a tensegrity hierarchy that eliminates those stresses by its very nature. Curves may appear at one level within a tensegrity hierarchy, but when looked at in more detail, have structural components that handle tension and compression in straight lines.
Undoubtedly, the fibre angle within any particular tissue depends on the functional context. The model in figure 8 shows struts arranged in a self-similar array and tension cables with differing orientations. Previous descriptions of “random” collagen orientations may have misinterpreted what were actually functionally ordered tensegrity alignments,91 and the sensitivity of newer imaging techniques and their analysis may resolve this.92,93
Helixes within helixes
Axial compression of a tensegrity helix initiates rotation in a direction dependent on the helical angle and strut orientation (chirality), with a corresponding decrease in the central diameter. Axial extension causes it to expand demonstrating a negative Poisson ratio; most man-made materials reduce their width when stretched,9,16 but this unusual response is common in biological structures.1,51 Surrounding a helix with another one of opposite chirality increases resistance to axial compression, as each helical layer counteracts the rotation of the other; crossed helixes have been shown to alter tubular properties.33,34
The intervertebral disc contains collagen arranged in concentric lamellae, with opposing orientations in alternate helical layers that provide tensile reinforcement.29 Whether this is a tensegrity configuration is yet to be assessed; but the widespread view that discs provide resistance to spinal compression as a prime function is probably too simplistic, and the whole spine has been looked at from a tensegrity perspective.51 Although disc failure usually occurs in tension,94 this is usually due to abnormal loading.
The negative Poisson ratio may also have relevance to the helical dynamics of the heart and has been described with the tensegrity ‘jitterbug’ mechanism. When any two tension triangles of a tensegrity ‘icosahedron’ are pushed together or pulled apart (Fig. 6c), the entire structure contracts and expands, respectively. 1,50,51,95
PUTTING THIS ALL TOGETHER
51,74,76 Helical ‘tubes within tubes’ mean that fascial compartments of the trunk and limbs can be considered in the same way. Objections that fascia is too flexible to contain compression struts can be overcome by considering the diameter of muscle, and its increase during contraction, as such struts. This would undoubtedly alter the tension pattern of surrounding fascia, which has itself been shown to influence the force appearing at tendons.39,40 In a tensegrity sense, fascia is the bodies main component of tension suspended between bones under compression, with smaller compartments taking origin from larger ones. Muscle fibres can then be considered as mere motors.
Helical and tensegrity structural systems complement each other, and are based on the fundamental properties of the tetrahedron and icosahedron. A chain of tensegrity icosahedra simply contains the crossed-helical fibres of a tube. Putting all this together from a helical-tensegrity perspective necessitates a reappraisal of structural biology and manual therapeutic techniques in terms of fundamental geometry.
CONCLUSION
The observation of a geometric pattern doesn’t necessarily imply anything meaningful, as Johannes Kepler (1571-1630) found out with his early description of a platonic solar system. However, the simple tetrahedron, octahedron, cube and hexagon are recognised in the structures of inorganic crystals, a result of atomic close-packing and principles of symmetry. (fig. 3b,c).1,4,50 Carbon fullerenes and viruses appear as icosahedra and are related to the geodesic geometry of a sphere(fig. 3d).1,2,23 The hexagonal packing of muscle fibrils and cells occurs because of the same physical laws.4,5,65 There are many possible consequences of close-packing, and the tetrahelix as one of them provides a more energy-efficient solution in molecular biology (fig. 5).53,54
Molecules assemble spontaneously and automatically balance the attraction and repulsion of their constituent atoms in a state of minimal-energy.24,79 The helix forms because of the same ‘platonic’ rules, those of organic chemistry and the dynamic nature of biological systems. The tetrahelix and its geometry then describe the helical hierarchies of protein structures and DNA.
Concurrent with the molecular helix is the principle of tensegrity. Tension and compression (attraction and repulsion); geodesic geometry and minimal-energy; and the inherent ability to form hierarchies are characteristics of both these structures. At the cellular level, the tensegrity principle describes the mechanical behaviour of the cytoskeleton, being a semi-autonomous system amenable to such analysis because of its size.5 As a structural mechanism, tensegrity depends on the integration of every part, and it has been proposed that this includes the whole body from molecules, cells, extra-cellular and fascial matrix to the entire musculo-skeletal system.1,4,5,74-76 Although it has been described at higher levels of anatomy, detailed multi-scale syntheses of its components are few. The helix, however, is a readily observable pattern at many different levels and may be inseparable from tensegrity, but there is a caveat.
If the structure of the human body is considered as a vast hierarchy of interacting sub-tensegrities, structurally and functionally, the examination of any part in isolation can be misleading, as it is inevitably incomplete.39-41 The possibilities for enquiry become virtually endless and make it unlikely that ‘bio-tensegrity’51 could ever be proved. However, if it describes biological systems more thoroughly, it is only a matter of time before this becomes the standard approach to biomechanics.
Human anatomy and physiology have been described in terms of tensegrity, and the volume of supporting evidence is steadily increasing. The helix is a well-known structural motif in biology. The fundamental links between tensegrity, the helix and platonic solids support a comprehensive view of human anatomy that is best appreciated as a complex interaction of natural physical forces.
ACKNOWLEDGEMENTS
Figures 1, 2, 3c reproduced from: Scarr GM. Simple geometry in complex organisms. J Bodyw Mov Ther 2010;14:424-44 with permission of Elsevier.
Figures 6a & b reproduced from: ‘Scarr GM. A model of the cranial vault as a tensegrity structure, and its significance to normal and abnormal cranial development. Int J Osteo Med 2008;11:80-9’ with permission of Elsevier.
REFERENCES
- Levin SM. The icosahedron as the three-dimensional finite element in biomechanical support. Proceedings of the Society of General System Research Symposium on Mental Images, Values and Reality pp G14-G26. Philadelphia. 1986.
- Dearden PK, Sowerby SJ. Physical law not natural selection as the major determinant of biological complexity in the subcellular realm: new support for the pre-Darwinian conception of evolution by natural law. BioSys 2003;71:297-303.
- Pauling L. The architecture of molecules. Proc Nat Acad Sci 1964;51:977-84.
- Scarr GM. Simple geometry in complex organisms. J Bodyw Mov Ther 2010;14:424-44.
- Ingber DE. Tensegrity-based mechanosensing from macro to micro. [Review] Prog Biophys Mol Biol 2008;9:163-79.
- Skelton RE, Adhikari R, Pinaud JP, Chan W, Helton JW. An introduction to the mechanics of tensegrity structures. Proc. 40th IEEE Conf. Decision and Contr 2001;5:4254-9.
- Masic M, Skelton RE, Gill PE. Optimization of tensegrity structures. Inter J Solids Struct 2006;43:4687-703.
- Standring S. (ed). Grays anatomy 39th ed. Elsevier Churchill Livingstone. 2005.
- Gordon JE. Structures, or why things don’t fall down. Penguin. 1978.
- Walker PMB. Editor, Chambers science and technology dictionary. Chambers. Edinburgh; 1988.
- Chouaib N, Goriely A, Maddocks JH. Helices. Proc Nat Acad Sci 2006;103:9398-403.
- Denton MJ, Marshall CJ, Legge M. The protein folds as platonic forms: new support for the pre-Darwinian conception of evolution by natural law. J Theor Biol 2002;219:325-42.
- Parry DAD, Fraser RD, Squire JM. Fifty years of coiled-coils and alpha-helical bundles: A close relationship between sequence and structure. J Struct Biol 2008;163:258-69.
- Orgel JPRO, Irving TC, Miller A, Wess TJ. Microfibrillar structure of type I collagen in situ. Proc Nat Acad Sci 2006;103:9001-5.
- Hulmes DJS, Wess TJ, Prockop DJ, Fratzl, P. Radial packing, order, and disorder in collagen fibrils. Biophys J 1995;68:1661-70.
- Lakes R. Materials with structural hierarchy. Nature 1993;361:511-5.
- Jelinek HF, Jones CL, Warfel MD, Lucas C, Depardieu C, Aurel G. Understanding fractal analysis? The case of fractal linguistics. Complexus 2006;3:66-73.
- Gao H, Ji B, Jager, Arzt E, Fratz P. Materials become insensitive to flaws at nanoscale: lessons from nature. Proc Nat Acad Sci 2003;100:5597-600.
- Gupta HS, Seto J, Wagermaier W, Zaslansky P, Boesecke P, Fratzl P. Cooperative deformation of mineral and collagen in bone at the nanoscale. Proc Nat Acad Sci 2006;103:17741-6.
- Puxkandl R, Zizak I, Paris O, Keckes J, Tesch, Bernstorff S et al. Viscoelastic properties of collagen: synchrotron radiation investigations and structural model. Phil Trans R Soc Lond B 2002;357:191-197.
- Salvadori M. Why buildings stand up: the strength of architecture. WW Norton; 1980: p83.
- Crick FHC, Watson JD. Structure of small viruses. Nature 1956;177:473-5.
- Caspar DLD. Movement and self-control in protein assemblies. Quasi-equivalence revisited. Biophys J 1980;32:103-33.
- Van Workum K, Douglas JF. Symmetry, equivalence, and molecular self-assembly. Phys Rev E Stat Non-lin Soft Matt Phys 2006;73:1-15.
- Holzapfel GA. Collagen in arterial walls: biomechanical aspects. In: Fratzl P, Editor. Collagen: structure and mechanics. Springer; 2008, pp. 285-324.
- Gabella J. The cross-ply arrangement of collagen fibres in the submucosa of the mammalian small intestine. Cell Tiss Res 1987;248:491-7.
- Carey EJ. Studies in the dynamics of histogenesis I. Tension of differential growth as a stimulus to myogenesis. J Gen Physiol 1920;2:357-72.
- Carey EJ. Studies in the dynamics of histogenesis II. Tension of differential growth as a stimulus to myogenesis in the esophagus. J Gen Physiol 1920:3:61-83.
- Hukins DWL, Meakin JR. Relationship between structure and mechanical function of the tissues of the intervertebral joint. Am Zool 2000;40:42-52.
- Avery NC, Bailey AJ. Restraining cross-links responsible for the mechanical properties of collagen fibers: natural and artificial. In: Fratzl, P. Editor. Collagen: structure and mechanics. Springer; 2008, p 81-110.
- Koob TJ, Long JH. The vertebrate body axis: evolution and mechanical function. Am Zool 2000;40:1-18.
- Etnier SA. Twisting and bending of biological beams: distribution of biological beams in a stiffness mechanospace. Biol Bull 2003;205:36-46.
- Clark RB, Cowey JB. Factors controlling the change of shape of certain nemertean and turbellarian worms. J Exp Biol 1958;35:731-48.
- Shadwick R. Foundations of animal hydraulics: geodesic fibres control the shape of soft bodied animals. J Exp Biol 2008;211:289-91.
- Gutsmann T, Fantner GE, Venturoni M, Ekani-Nkodo A, Thompson JB, Kindt JH, et al. Evidence that collagen fibrils in tendons are inhomogeneously structured in a tube-like manner. Biophys J 2003;84:2593-8.
- Purslow PP. The extracellular matrix of skeletal and cardiac muscle. In: Fratzl P, Editor Collagen: structure and mechanics. Springer; 2008, p. 325-353.
- Buckberg GD. Basic science review: the helix and the heart. J Thorac Cardiovasc Surg 2002;124:863-83.
- Grosberg A. A bio-inspired computational model of cardiac mechanics: pathology and development. PhD.thesis, California Institute of Technology, Pasadena, California.
- Maas H, Jaspers RT, Baan GC, Huijing PA. Myofascial force transmission between a single muscle head and adjacent tissues: length effects of head of rat EDL. J Appl Physiol 2003;95:2004-13.
- Huijing PA, Baan GC. Myofascial force transmission via extramuscular pathways occurs between antagonistic muscles. Cells Tiss Org 2008;188:400-14.
- Stecco A, Macchi V, Stecco C, Porzionato A, Day JA, Delmas V, et al. Anatomical study of myofascial continuity in the anterior region of the upper limb. J Bodyw Mov Ther 2009;13:53-62.
- Passerieux E, Rossignol R, Letellier T, Delage JP. Physical continuity of the perimysium from myofibers to tendons: involvement in lateral force transmission in skeletal muscle. J Struct Biol 2007;159:19-28.
- Kier WM, Smith KK. Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrostats. Zool J Linn Soc 1985;83:307-24.
- Johnson S, Kier WM. Intramuscular crossed connective tissue fibres: skeletal support in the lateral fins of squid and cuttlefish (Mollusca: Cephalopoda). J Zool Lond 1993;231:311-38.
- O’Reilly JC, Summers AP, Ritter DA. The evolution of the functional role of trunk muscles during locomotion in adult amphibians. Am Zool 2000;40:123-35.
- Hebrank MR. Mechanical properties and locomotor functions of eel skin. Biol Bull 1980;158:58-68.
- Pabst DA. To bend a dolphin: convergence of force transmission designs in cetaceans and scombrid fishes. Am Zool 2000;40:146-55.
- Stecco L. Fascial Manipulation for Musculoskeletal Pain. Piccin Nuova Libraria, Padova; 2004.
- Sergueef N. Cranial osteopathy for infants, children and adolescents. Churchill Livingstone Elsevier; 2007.
- Fuller BB. Synergetics, Explorations in the Geometry of Thinking. Macmillan; 1975.
- Levin SM. The tensegrity truss as a model for spine mechanics: biotensegrity. J Mech Med Biol 2002;2:375-88.
- Pickett GT. Gross M, Okuyama H. Spontaneous chirality in simple systems. Phys Rev Letts 2000;85:3652-5.
- Sadoc JF, Rivier N. Boerdijk-Coxeter helix and biological helices as quasicrystals. Mat Sci Eng 2000;294-6:397-400.
- Lord EA. Helical structures: the geometry of protein helices and nanotubes. Struct Chem 2002;13:305-14.
- Galloway J. Helical imperative: paradigm of form and function. Encyc. Life Sci. (online) Wiley Interscience. 2002.
- Pauling L, Corey RB, Branson HR. 1951. The structure of proteins: two hydrogen-bonded helical configurations of the polypeptide chain. Proc Nat Acad Sci 1951;37:205-11.
- Jones LJF, Carballido-Lopez R, Errington J. Control of cell shape in bacteria: helical, actin-like filaments in Bacillus subtilis. Cell 2001;104:913-22.
- Shih Y, Rothfield L. The bacterial cytoskeleton. Microbiol Mol Biol Rev 2006;70:729-54.
- Lloyd C, Chan J. Helical microtubule arrays and spiral growth. Plant Cell 2002;14:2319-24.
- Douady S, Couder Y. Phyllotaxis as a physical self-organized growth process. Phys Rev Letts 1992;68:2098-101.
- Atela P, Gole C, Hotton S. A dynamical system for plant pattern formation: a rigorous analysis. J Nonlinear Sci 2002;12:641-76.
- Gibson CM, Gibson WJ, Murphy SA, Marble SJ, McCabe CH, Turakhia MP et al. Association of the Fibonacci cascade with the distribution of coronary artery lesions responsible for ST-segment elevation myocardial infarction. Am J Cardilo 2003;1:595-7.
- Stewart I. Life’s other secret. Allen Lane, Penguin; 1998.
- Ingber DE, Madri JA. Jamieson JD. Role of basal lamina in neoplastic disorganization of tissue architecture. Proc Nat Acad Sci 1981;78:3901-5.
- Levin SM. Continuous tension, discontinuous compression: a model for biomechanical support of the body. Bull Struct Integ 1982;8.
- Joshi HC, Chu D, Buxbaum RE, Heidemann SR. Tension and compression in the cytoskeleton of PC 12 neurites. J Cell Biol 1985;101:697-705.
- Van Essen DC. A tension-based theory of morphogenesis and compact wiring in the central nervous system. Nature 2007;385:313-8.
- Du N, Liu XY, Narayanan J, Li L, Lim, Li D. Design of superior spider silk: from nanostructure to mechanical properties. Biophys J 2006;91:4528-35.
- Frantsevich L, Gorb S. Arcus as a tensegrity structure in the arolium of wasps (Hymenoptera: Vespidae) Zoology 2002;105:225-37.
- Moore KA, Polte T, Huang S, Shi B, Alsberg E, Sunday ME, Ingber DE. Control of basement membrane remodeling and epithelial branching morphogenesis in embryonic lung by Rho and cytoskeletal tension. Dev Dyn 2005;232:268-81.
- Watson RR, Fu Z, West JB. Morphometry of the extremely thin pulmonary blood-gas barrier in the chicken lung. Am J Physiol – Lung Cell Mol Phys 2007;292:L769-77.
- Weibel ER. How to make an alveolus. Eur Resp J 2008;31:483-5.
- Maina JN. Spectacularly robust! Tensegrity principle explains the mechanical strength of the avian lung. Resp Physiol Neurobiol 2007;155:1-10.
- Ingber DE. Cellular mechanotransduction: putting all the pieces together again. FASEB J 2006;20:811-27.
- Levin SM. Putting the shoulder to the wheel: a new biomechanical model for the shoulder girdle. J Biomed Sci Instrum 1997;33:412-7.
- Parker KK, Ingber DE. Extracellular matrix, mechanotransduction and structural hierarchies in heart tissue engineering. Phil Trans Roy Soc B Biol Sci 2007;2114:1-13.
- Levin SM. A suspensory system for the sacrum in pelvic mechanics: biotensegrity. In: Vleeming A, Mooney V, Stoeckart R, Editors. Movement, Stability and Lumbopelvic Pain. Churchill Livingstone; 2007.
- Scarr GM. A model of the cranial vault as a tensegrity structure, and its significance to normal and abnormal cranial development. Int J Osteo Med 2008;11:80-9.
- Connelly R, Back A. Mathematics and tensegrity. Am Scien 1998;86:142-51.
- Zanotti G, Guerra C. Is tensegrity a unifying concept of protein folds? FEBS Letters 2003;534:7-10.
- Sung LA, Vera C. Protofilament and hexagon: A three-dimensional mechanical model for the junctional complex in the erythrocyte membrane skeleton. Ann Biomed Eng 2003;31:1314-26.
- Zhu Q, Vera C, Asaro RJ, Sche P, Sung LA. A hybrid model for erythrocyte membrane: a single unit of protein network coupled with lipid bilayer. Biophys J 2007;93:386-400.
- Mazumder A,Shivashankar GV. Emergence of a prestressed eukaryotic nucleus during cellular differentiation and development. J Roy Soc Interface 2010;7:S321-S30.
- Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS. Emergent patterns of growth controlled by multicellular form and mechanics. Proc Nat Acad Sci 2005;102:11594-9.
- Henderson JH, Carter DR. Mechanical induction in limb morphogenesis: the role of growth-generated strains and pressures. Bone 2002:31:645-53.
- Ingber DE, Folkmann J. Mechanochemical switching between growth and differentiation during fibroblast growth factor-stimulated angiogenesis in vitro; role of extracellular matrix. J Cell Biol 1989;109:317-30.
- Ingber DE. Control of capillary growth and differentiation by extracellular matrix: use of a tensegrity (tensional integrity) mechanism for signal processing. Chest 1991;99:34-40.
- Watermann-Storer CM, Salmon WC, Salmon ED. Feedback interactions between cell-cell adherens junctions and cytoskeletal dynamics in newt lung epithelial cells. Mol Biol Cell 2000;11:2471-83.
- Dejana E, Corada M, Lampugnani MG. Endothelial cell-to-cell junctions. FASEB J 1995;9:910-8.
- De Catarina R, Massora M, Libby P. Endothelial functions and dysfunctions. In: De Caterina, R., Libby, P. Editors. Endothelial dysfunctions in vascular disease. Wiley-Blackwell; 2007.
- Jimenez-hamann MC, Sacks MS, Malinin TI. Quantification of the collagen fibre architecture of human cranial dura mater. J Anat 1998;192:99-106.
- Angelsky OV, Tomka YY, Ushenko AG, Ushenko YG, Ushenko YA. Investigation of 2D Mueller matrix structure of biological tissues for pre-clinical diagnostics of their pathological states. J Phys D Appl Phys 2005;38:4227-35.
- Williams RM, Zipfel WR, Webb WW. Interpreting second-harmonic generation images of collagen I fibrils. Biophys J 2005;88:1377-86.
- Ker RF. Damage and fatigue. In: Fratzl P. editor. Collagen: structure and mechanics. Springer. 2008, p. 111-132.
- Verheyen HF. The complete set of jitterbug transformers and the analysis of their motion. Comp Maths Appl 1989;17:203-50.
